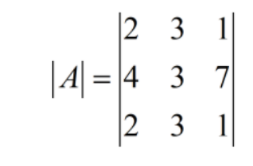Minors, Co-Factors And Applications Of Determinants

We will study about the minors and cofactor calculation of a given determinant. We will take the example of a 3×3 matrix and calculate the minors and cofactors of the determinant. This method can be applied to 3×3 or higher order determinants. We will learn about the relationship between minors and cofactors of the determinant. At the end, we will learn the calculation of the area of a triangle by determinant method.

Minors of Determinant

If we have a determinant |A| of size n, then the minor of any element aij can be obtained by deleting the ith row and jth column in which the aij stands. The minor of any element is represented by Mij. 

To understand the above explanation, let’s assume a 3×3 determinant 

a11 = 2 ; a12 = 3 ; a13 = 1

a21 = 4 ; a22 = 3 ; a23 = 7

a31 = 2 ; a32 = 3 ; a33 = 1

So, the minors of determinant |A| are:

M11 (deleting 1st row and 1st column) = 3 7 1 3   = 3*3 – 1*7 = 2

M12 (deleting 1st row and 2nd column) = 4 7 2 3   = 4*3 – 2*7 = -2

M13 (deleting 1st row and 3rd column) = 4 3 2 1   = 4*1 – 2*3= -2

M21 (deleting 2nd row and 1st column) = 3 1 1 3   = 3*3 – 1*1 = 8

M22 (deleting 2nd row and 2nd column) = 2 1 2 3   = 2*3 – 2*1 = 4

M23 (deleting 2nd row and 3rd column) = 2 3 2 1   = 2*1 – 2*3 = -4

M31 (deleting 3rd row and 1st column) = 3 1 3 7   = 3*7 – 3*1 = 18

M32 (deleting 3rd row and 2nd column) = 2 1 4 7   = 2*7 – 4*1 = 10

M33 (deleting 3rd row and 3rd column) = 2 3 4 3   = 2*3 – 4*3 = -6

Cofactors of Determinant

The cofactor is a minor with sign ( + or – ).The cofactor of aij is represented by Aij and is defined as (-1)i+j Mij.

To understand the above explanation, let’s assume a determinant

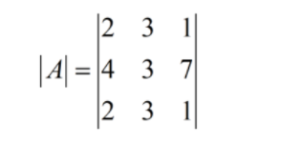
a11 = 2 ; a12 = 3 ; a13 = 1

a21 = 4 ; a22 = 3 ; a23 = 7

a31 = 2 ; a32 = 3 ; a33 = 1

For minors, we can refer to the previous calculations of minors.

Cofactors of determinant A can be obtained as follows:

A11 = (-1)1+1M11 = 2

A12 = (-1)1+2M12 = -2

A13 = (-1)1+3M13 =-2

A21 = (-1)2+1M21 = -8

A22 = (-1)2+2M22 = 4

A23 = (-1)2+3M23 = 4

A31 = (-1)3+1M31 = 18

A32 = (-1)3+2M32 = -10

A33 = (-1)3+3M33 = -6

Area of Triangle in Determinant Form

If the triangle is a right-angle triangle, then finding the area of a triangle is not difficult because the area of such a triangle can be calculated by finding the product of one-half of the base and the height. But if the given triangle is not a right-angle triangle, then calculating the area of the triangle is not that easy. In this case, we can use the determinant method to calculate the area of the triangle.

The area of a triangle in determinant form can be calculated if the vertices of the triangle are known. We use a general formula for the area of a triangle is half the product of the base of the triangle and the height of the triangle from the base. But in coordinate geometry, we follow a different approach for the calculation for the area of the triangle. If the coordinates of the vertices of a triangle are known, then we can calculate the area of the triangle in determinant form. The formulation of the area of a triangle in determinant form gives a scalar value that can be positive or negative. But we consider the absolute value of the determinant as the area of the triangle because the area of a triangle can never be negative. Now, if the vertices of a triangle ABC are A(a, b), B(p, q), and C(x, y) in a Cartesian plane, then the area of this given triangle in determinant form’s formula is given by

Area of Triangle,

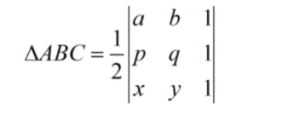
= 12 [aq-y-pb-y+xb-q]

We will take one example to understand the above formulation. Let’s consider a triangle with vertices A (2,3) , B(1,2) and C(4,5).

So, by using the above formulation,  we can calculate the area of the given triangle  as,

Area of Triangle ∆ABC 

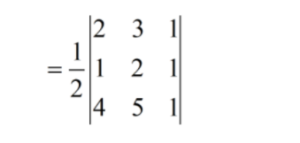
= 12 22-1-13-5+43-2=8

Conclusion

We have learned about the calculation of minors and cofactors of the given determinant. We have learned that the minor of an element is the determinant obtained by excluding the row and column of the given element. The cofactor of an element is the product of the minor of the element with -1 to the power of the sum of numbers associated with the row and column of the element. We have calculated the minors and cofactors by taking the example of a determinant. We have also learned the calculation of the area of a triangle by using the determinant method. This method of area calculation is very useful in calculating the area of a triangle that is not a right-angle triangle.