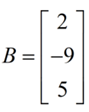Matrix Notation

In this article we will study about the basic notation used in the matrix. We will learn about the representation of a particular element of a given matrix. Then we will learn about the representation of various types of matrices like row vector, column vector, identity matrix, symmetric matrix, one vector and transpose of a matrix. We will also learn to represent the operation of the matrices. These are very important for the analysis of data given in matrix as while doing calculations it becomes easy for us to enter the data and take the data.

A matrix is a rectangular array of elements. These elements are arranged in rows and columns. If a matrix “m” rows and “n” columns then it is said to be a matrix of order m x n. A matrix is generally represented by a capital letter printed in a bold font i.e. A, P, Z. Lower case letters with a double subscript ( i.e. 𝑎𝑗𝑘, p𝑗𝑘, z𝑗𝑘) are used to represent the elements of a matrix. We can understand this by taking one example of any matrix as follows:

In the above matrix A, the number of rows are 2 and the number of columns are 3 so it is a (m=) 2 x (n=)3 matrix.

a11 = 2 ;  i = 1 and j = 1 , element belongs to 1st row and 1st column.

a12 = -3 ; i = 1 and j = 2 , element belongs to 1st row and 2nd  column.

a13 = 1.5 ; i = 1 and j =31 , element belongs to 1st row and 3rd  column.

a21 = 7 ;   i = 2 and j = 1 , element belongs to 2nd row and 1st column.

a22 = 3 ; i = 2 and j = 2 , element belongs to 2nd  row and 2nd column.

a23 = -2 ; i = 2 and j = 3 , element belongs to 2nd row and 3rd  column.

Row vector and Column vector matrix 

A matrix of the order of 1xm is known as a row vector matrix and if the order of the matrix is nx1 then it is known as column vector matrix . 

For example, A = 2 -9 5 , is a row vector matrix of the order 1×3 , i.e. 1 rows and 3 columns.

Similarly,

  , is a column vector matrix of the order 3×1 i.e. 3 rows and 1 column.

Square Matrix and Diagonal Matrix

A matrix in which the number of rows is equal to the number of columns is known as a square matrix. A square matrix in which except for the diagonal elements other elements are zero is called a diagonal matrix. The diagonal matrix is generally represented by D

We will understand by the following example.

Symmetric matrix

A square matrix in which the mnth element and nmth element are the same is called a symmetric matrix. It is generally represented by S.

For example, 

Transpose of a matrix

The transpose of a matrix A is represented by A’ or AT. We have to interchange rows and columns to get the transpose of a matrix.

Now, to perform addition or subtraction we need to add or subtract corresponding elements of matrices i.e. in the above matrices P and Q , p21 will be added or subtracted to q21. To understand this let’s do the addition of matrices first and then we will do subtraction.

  Matrix multiplication by Scalar

In this we multiply each element of the given matrix by a scalar. We represent scalar by italicized lowercase letters in a non-bold font. 

If  A is a matrix and b is a given scalar then matrix multiplication of A by b is represented by bA.

Subtraction of a scalar from Matrix 

If we have a matrix of order m x 1 then, the subtraction of a scalar from a matrix is obtained by first multiplying the scalar by an m x 1 one vector and then taking the difference of these two vectors.It is represented by A-m1.

For example, if we have a matrix A = 2 -9  5   and scalar is 2, then to subtract this scalar from the given matrix A,

= 2 -9 5 – 21 1 1

  = 2-2 -9-2 5-2  

 = 0 -11 3

Conclusion

In the above article, we learned the various notations used for matrix and matrix operations. These are basic notations used for the matrix. We learned the notation of a particular element in the matrix entry. This is very important because while doing calculations, and data entry it becomes easy for us to enter the data or get the data directly by using these notations. We also learned about the notation of row vector and column vector matrix along with notation for square matrix, diagonal matrix, symmetric matrix, one vector, and the transpose of a matrix.