Introduction to Linear Programming

• Linear programming helps to solve complex problems with simple assumptions
• Linear programming is a simple technique where we can even solve complex problems.
• Nowadays, we can find every application of Linear programming. For example, while you return home from the office in the car, finding the shortest way to reach the home is one of the linear programming applications.
• LP(linear programming) always keeps the complex problem simple and in the easiest form. 
• We can convert all the complex problems into simple problems through linear functions.

LINEAR PROGRAMMING MEANING

• The linear program is used to find the best result from the linear function. It is one of the best methods to perform to obtain optimum values by making a few assumptions.
• Nowadays, it is used in

1. telecommunication industries
2. transportation industry
3. in energy production
4. manufacturing industries

• It provides the simplest way to solve the complicated problems occurring in the world by the linear functions
• Linear programming objective consists of two things. they are

1. linear equality
2. inequality constraints

• To get a better outcome, one needs to minimize and maximize the above two linear functions.

LINEAR PROGRAMMING EXAMPLE

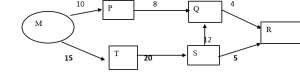
Suppose a pizza delivery man has to deliver pizza to 6 houses from MCDonalds (From location M) to different houses (P, Q, R, S, T). The distance from

• MC Doland’s (From position M) to house P is 10km
• From house P to House Q is 8 Km
• From house Q to house R is 7 Km
• From M to house T is 15 km
• From house T to house S is 20 km
• From house S to House Q is 12km

Like the below diagram, the pizza delivery man should find the best and shortest way to deliver the pizza to save fuel and time. This example is one of the best of Linear programming. Operation Research is the process where one can choose the best routing. It describes how to make things simple, here in the above case, pizza delivery. 

COMPONENTS OF LP(LINEAR PROGRAMMING)

Some of the basic components involved in Linear programming are

1. Decision variables
2. constraints
3. data
4. objective functions

CHARACTERISTICS OF LP(LINEAR PROGRAMMING)

Here are some of the characteristics involved in linear programming. They are

1. Constraints
2. Objective functions
3. Linearity
4. Finiteness
5. Non- negativity
6. Decision variables

CONSTRAINTS – The limitation should be expressed in the mathematical form

OBJECTIVE FUNCTIONS – The objective function should be specified in number and values(quantitative) rather than qualitative.

LINEARITY- The relationship between the two variables must be one.

FINITENESS – The outcome should have finite and infinite output and input. If the function is provided with infinite input, then the process is completely not feasible.

NON NEGATIVITY – The variable values should not be negative. It should always be positive or zero.

DECISION VARIABLE – The decision variable should be chosen correctly to solve the problems.

FORMULA OF LINEAR PROGRAMMING

The linear programming problems contain all the above-mentioned data.

• The decision variable – x and y decide the outcome of LP
• The objective function – z will minimize and maximize the objective functions to get the outcome
• To limit the decision variable, constraints and restrictions are used.
• Make sure the decision variable should be positive

The general formula of LP

1. Objective function (Z) = px + qy
2. Constraints = cx + dy ≤e, fx + gy≤ h. represents inequality
3. Non – negative restrictions = x ≥0, y ≥0

STEPS TO SOLVE LINEAR PROGRAMMING PROBLEMS

Here are some of the simple ways to solve the linear programming problem. The steps are given below.

• Step 1 – Choose the decision variables.
• Step 2 – apply all the values in the objective functions and later decide whether to minimize or maximize the function.
• Step 3 – list out all the constraints
• Step 4 – ensure the decision variable is non-negative(positive or zero)
• step 5 – choose either simplex or graphical method to solve the linear programming problems.

LINEAR PROGRAMMING METHOD

There are two methods to solve the problem of linear programming. They are 

1. Simplex method
2. Graphical method

LINEAR PROGRAMMING BY SIMPLEST METHOD

It is applied when the equation has two or more decision variables

Here are the objective functions that need to be maximized and the constraints. The steps are given below

Step 1: Addition of slack variables for the conversion of inequalities into equations. Here Y1 and Y2 are considered as slack variables

Step 2 Construct the simplex matrix with the given equation given in the question. Form an augmented matrix to solve the equation.

Step 3: identify the column which has the highest negative value. That helps to find out the pivot column.

Step 4: divide the column right behind the Z column by the number in the pivot column. The negative number in the last row indicated the objective function coefficients.

Step 5: using matrix properties, make all the elements in the pivot column as 0. By subtracting with other rows and columns

step 6: ensure the bottom-most columns have the first two entries is zero. The last row should be non-negative

Step 7: find the solution from the augmented matrix

GRAPHICAL METHOD

• Here two-variable linear programming can be found
• We can minimize and maximize the values for two decision variables to find the solutions.
• constraints are listed out and added to the variables
• The inequalities are added to the XY plane
• The intersecting region in the graph is considered a feasible region
• This feasible region only provides the solution to the problem. 

STANDARD FORM

Here are some of the step to followed before doing the problem

1. First step maximize

For example F(x1, x2) = (q2 x2 + q2 x2)

1. Constraints

P11X1 + P12X2  ≤ b1

P21X1 + P22X2  ≤ b2

P31X1 + P32X2  ≤ b3

1. Non- negative variable

x, y ≥ 0

Example

suppose the manufacturer has the unit, say M km2, to make dark chocolate and white chocolate or some combination of two. The manufacturer has a limited amount of Cocco C kg and Sugar S kg. While 

• dark chocolate need – C1 kg of Cocco and S1 kg of sugar
• White chocolate need – C2 kg of Cocco and S2 kg of sugar
• P1 is the selling price of dark chocolate, and P2 is the selling price of white chocolate
• If we denote the quantity of Dark and white chocolate produced is x1 and x2. Express the problem in standard form.

Solution:

The maximum revenue is dark and white chocolate sales

P1. x1  + P2. x2  

The limit on production quantity is x1 + x2 ≤M

Limit on cocco C1. x1  + C2. x2 ≤ C

Limit on sugar S1. x1  + S2. x2 ≤ S

No negative on product x1, x2 ≥ 0

APPLICATION OF LINEAR PROGRAMMING

It has been used in many industries. Here are some of the industries where linear programming are mainly used

• LP(Linear programming) plays a major role in analyzing the supply chain operation in manufacturing industries. The main motto of this operational unit is to increase efficiency in a simple way and at an easy cost. Here linear programming comes up with the layout model for easy storage and packing. It reduces the burden of the workload. Many US-based warehouses are using linear programming technology for easy storage.
• Linear programming also came up with a new model to attract customers. Like Walmart, reliance and many stores all across the world come across this model to gain more customization. It provides an idea about self space.
• We have already seen an example above. It helps many companies by offering easy delivery routes. It helps the salesman in many ways. The delivery man should find the best and short way to deliver the products to save fuel and time. This example is one of the best of Linear programming. 
• It is also used in machine learning technology to predict the values.