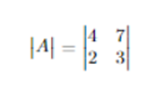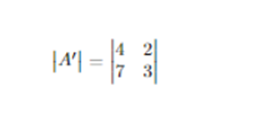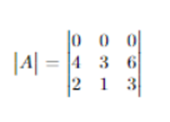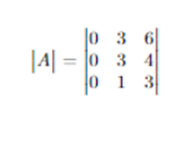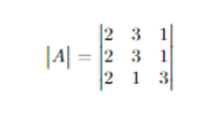We will study the fundamentals of determinants and the calculation of determinants of a matrix along with the representation of a matrix. We will take examples to understand the fundamentals of determinants. We will discuss the minors and cofactors of a determinant. and learn about the minor and cofactor calculation by examples. We will also study the properties of determinants like reflection property, triangle property, all zero property, sum property, scalar multiple property, factor property, property of multiplication, property of power, and property of proportionality.

Definition of Determinants

A number associated with a square matrix of order ‘n’ is known as the determinant of the given matrix. This number can be a real number as well as a complex number depending upon the entries of the square matrix. In other words, we can define a determinant as a scalar value which can be calculated from the elements/entries of a square matrix. The determinant method is very useful in finding the solution of simultaneous linear equations, area of a triangle, etc.

To understand the method to find determinants, let’s assume a square matrix A of size 2 x 2.

The standard method to represent the determinant is, 

Minors and Cofactors of Determinant

If we have a determinant |A| of size n, then the minor of any element aij can be obtained by deleting the ith row and jth column in which the aij stands. Minor of any element is represented by Mij. The cofactor is a minor with sign ( + or – ). The cofactor of aij is represented by Aij and is defined as (-1)i+j Mij.

To understand the above explanation, let’s assume a determinant

Properties of Determinants

The following are the common properties of determinants:

  1. Reflection property – Determinants do not change on interchanging rows and columns i.e. when rows are transformed into columns and columns are transformed into rows, determinants do not change.

Example: If we have 

 then det(A) or |A| = -2

Now, interchanging rows and columns gives 

then |A’| = -2

  1. Triangle property – If all elements of a determinant above or below the main diagonal are zeroes, then the determinant of the given matrix is equal to the product of diagonal elements.

Example: If A is a determinant with all elements below diagonal are zero i.e. 

then ,|A| = 2*3*3 = 18

Now, if A is a determinant with all elements above diagonal are zero i.e. 

then ,|A| = 2*3*3 = 18

  1. All zero property – The determinants will be equal to zero if each term of rows or columns are zero.

Example: If we have

 

then det(A) or  |A| = 0

Now, for 

 then det(A) = |A| = 0

  1. Sum property – The determinant is said to possess the sum property, if few elements of row or column elaborated as sums of the determinants.
  2. Scalar multiplication property – If all the elements of any row (or any column) of a determinant are multiplied by a scalar (non-zero constant), then the determinant gets multiplied by the same scalar.

Example: If A = 

  then |A| = (aq-pb).

Now, multiplying 1st row of A by a scalar ‘m’, the new matrix 

Then |B| = maq-mpb = m(aq-pb) = m|A|

  1. Factor property – When we put x=a, and the determinant becomes zero, then we can say that (x–a) is the factor of the determinant.
  2. Multiplication property – If two matrices are multiplied, then the determinants of the obtained matrix is equal to the product of their individual determinants, i.e. det(AB) = det(A) X det(B)
  3. Property of Power – det(An) = [det(A)]n
  4. Property of Proportionality – If we have a matrix such that two rows or columns are the same to each other, then the determinant of that matrix is zero.

Example: if

 

  then 

|A| = 2( 3*3-1*1) – 3(2*3 – 2*1) + 1(2*1 – 2*3) 

= 16-12-4

 = 0

Conclusion

We have studied the determinant of a matrix. It is a number (may be positive, negative or complex) which is obtained by solving the matrix. This determinant is valid only for square matrices. We have also studied the properties of determinants like reflection property, triangle property, all zero property, sum property, scalar multiple property, factor property, property of multiplication, property of power, and property of proportionality. We have also studied determinants with examples. Although we discussed only 2 x 2 and 3 x 3 matrices, it can be applied to matrices of any order.