Profile
Settings
Refer your friends
Sign out
Definition of geometric progression?
A geometric progression (GP) is a non-zero numerical sequence. Each term after the first is determined by multiplying the preceding one by a fixed, non-zero value known as the common ratio. The sequence 2, 6, 18, 54,…, for example, is a geometric progression with a common ratio of 3. Similarly, a geometric sequence with a common ratio of ½ is 10, 5, 2.5, 1.25, etc.
Let us learn about geometric progression examples.
Types of Geometric Progression
- Finite Geometric Progression
- Infinite Geometric Progression
Finite Geometric Progression
A geometric progression with a finite number of terms or with finite sum is called a finite geometric progression. The last term should be defined in this type of progression. For example, 1/3, 1/6, 1/9, ….1/2187 is a geometric series with a finite number of terms where the last term is 1/2187.
Infinite Geometric Progression
There are an infinite number of terms in an infinite geometric progression. Here the last term should not be defined. For instance, 3, -6, +12, -24, +… is a geometric series with an infinite number of terms or we don’t know the last term.
Geometric Progression Formula
In order to find the nth term of a series we use the geometric progression formula. We need the common ratio and first term to find the nth term. If you don’t know the common ratio, you can figure it out by dividing any term by its previous term. The geometric progression formula for finding the nth term of the geometric Progression is:
Here,
The first term of the series is a, and the common ratio is r.
The total number of series is n.
Geometric Progression Sum Formula
In order to find the sum of geometric progression with a finite number of terms we use the basic sum formula . As we saw in the last part, there are two types of geometric progressions: finite and infinite geometric progressions. Thus, different formulas are used to calculate the sum of different series.
Finite Geometric Series
A finite geometric series can be defined as the sum of a finite geometric sequence. The formula that is used to find finite geometric series is:
The first term of the series is a, and the common ratio is r. The total number of series is n.
Infinite Geometric Series
Geometric progression sum to infinity series is used when the number of terms in a geometric progression is unlimited. Depending on the value of r, there are two situations in an infinite series.
Case 1: When| r| <1
S∞ = a ⁄ 1-r
Where,
- a is the first term
- r is the common ratio
Case 2
When| r| >1
In this case, the series has no sum.
Properties of Geometric Progression
- If every term of a geometric progression is multiplied or divided by a non-zero number, then the resulting terms are also geometric progression.
- If all the terms of GP are raised to the same powers, then the resulting terms are also in GP.
- If y² = xz, then three non-zero terms x, y, and z are in GP.
Arithmetic and Geometric Progression
The arithmetic progression (AP) is the mathematical operation that deals with numbers. Arithmetic is a popular sequence as well as geometric. If the difference between any two consecutive terms is similar, it is known as arithmetic progression. If the ratio of any two consecutive terms is always similar, it is known as geometric progression. In arithmetic progression, we use subtraction and addition to find terms, and in geometric progression we use division and multiplication to find terms. There are various geometric progression examples in the following section.
Examples of Geometric Progression
Here are a few geometric progression examples to get a better idea.
- Find the 5th term of the Geometric Progression 3,6,12………
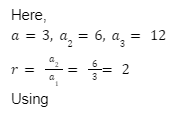
Conclusion
In this article, we learnt about the examples of geometric progression. If the ratio of any two consecutive terms is always the same, a sequence of numbers is called a geometric progression. The next number in the series is calculated by multiplying a set number by the preceding number.
A geometric progression’s product is the sum of all terms. It may be rapidly calculated by raising the geometric mean of the progression’s first and last individual terms to the power of the number of terms.
MS 3047, a clay tablet from Mesopotamia’s Early Dynastic Period, features a geometric progression with base 3 and multiplier ½. It’s been argued that it’s Sumerian and comes from Shuruppak. It’s the only known example of geometric progression before Babylonian mathematics.
