A straight line with no width can also be thought of as an infinite dimensional figure. It’s a collection of infinite points with the two sides of each point connected. In this we do not get to see any kind of curve. It is generally seen as horizontal, vertical or oblique. If an angle is measured between any two points of a straight line on the plane, then we get 180-degrees. One can see many examples of straight lines in our daily life as well, In which there can be mainly railway tracks, rulers, some parts of the road made of stairs, etc. Through this article, we will learn about the straight line and some equations related to it, which are described below.
What is a Straight Line?
A straight line is an infinitely long line that has nothing to do with a curve. It is constructed between two points on a plane, these ends can be anywhere in infinity. A straight line has no end point, which we can understand by taking the example of railway tracks. It is a straight figure which consists of two points X (a1, b1) and Y (a2, b2) between them, we can extend it to infinity. It is better represented in the figure below, which are as follows;
Types
There are mainly three types of straight lines, which are mainly classified on the basis of alignment. Alignment mainly refers to angles, which are made primarily along the x-axis or y-axis. Here they are described in their context, which are as follows;
Horizontal line- A line drawn horizontally is called a horizontal line, it is mainly drawn parallel to the x-axis and perpendicular to the y-axis. With the x-axis, they make a 00or 1800 angle, and with the y-axis, they form a 900 or 2700 angle.
Vertical line- A line drawn vertically is called a vertical line, it is mainly drawn parallel to the y-axis and perpendicular to the x-axis. With the y-axis, they make a 00or 1800 angle, and with the x-axis, they form a 900 or 2700 angle.
Oblique or Slanted lines- The lines which are drawn diagonally are called Oblique or Slanted lines. It makes many angles other than zero, ninety, one hundred eighty, two hundred and seventy.
Properties
Straight lines have their own merits which must be taken into account when using them, which are as follows;
- It is almost impossible to calculate the distance of a straight line between two extreme points because its length is infinite.
- Since the straight line has infinite length, it gives zero area, zero volume.
- It represents a one dimensional figure.
- A straight line does pass through two points, but we can represent an infinite number of points in it.
Equation Of a Straight Line
The main relation of the equation of a straight line is that linear equation on which it can be represented differently on the basis of the known variables, angles and constants of a straight line on the Cartesian plane. Apart from this, it tells the slope of the straight line and also describes its direction. It is calculated based on the y coordinate and the x coordinate, also called run over run. The equation of a straight line can also be represented as follows;
A straight line’s general equation is ax + by + c = 0, where ax + by + c = 0.
- where a, b, and c are constants, and a, b, and c are variables.
- Variables are x and y.
- -a/b is the slope.
Slope and Y-intercept Form
If the slope of a straight line is m = tanθ, the angle formed by the line with the positive x-axis is provided by: y = mx + b, where m is the slope, and the y-intercept is given by:
If, y = mx + b, where m is the slope.
Slope Point Form
If the slope of a straight line is m = tanθ,
Slope Point Form as, where is the angle produced by the line with the positive x-axis and
passing through a point (x1, y1)
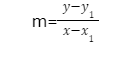
Two point form
If a straight line passes through these two points (x1, y1) and (x2, y2), then their equation will be as follows;
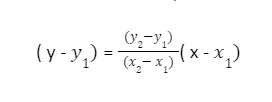
Intercept Form
If the x-intercept is a and the y-intercept is b, then point A is perpendicular to the x-axis and point B is horizontal on the y-axis.
Intercept form is ;


Lines parallel to the X-axis or the Y-axis equation
- If the equation of a line is y = ± a , then it is said to be parallel to the x – axis , where a denotes the distance from the x axis , if a lies above the x axis , then it will give the positive sign , and if below , then the value of a will be negative.
- If the equation of a line is x = ± b , then it is said to be parallel to the y – axis , where b denotes the distance from the y axis , will give the positive sign if b lies above the y axis , and if below , then the value of b will be negative.
Conclusion
The use of straight lines is not only useful for subjects like maths, but has also been considered necessary in the medical and industrial fields. It is used to show the correct position in the form of a graph. Along with this, it is also used in the research process and preparation of government budgets.In the article we learnt many things like its equation, slope,different types of straight lines and much more.Straight lines are a very important topic in competitive exams.Hope you liked the article.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






