In a square matrix, we can find a scalar value which can help us to find the adjoint and inverse of any square matrix. This value is known as determinant. The determinants help us find whether the square matrix is invertible or not. Also, they help us to calculate the cross- product of two vectors. The determinant of any matrix can be found by using some basic rules. We are going to learn about some basic rules to find determinants, properties and applications of determinants.

Determinants 

A scalar value that can be obtained from the elements present in a square matrix is known as a determinant. We can define the determinant as: for every square matrix of order m x m, there exists a scalar value which can be ascertained by the elements of the matrix ‘ . It is denoted by det(A) or |A|. Instead of using a square bracket, the numbers of determinants are enclosed in two bars.For example, let us consider a matrix ,

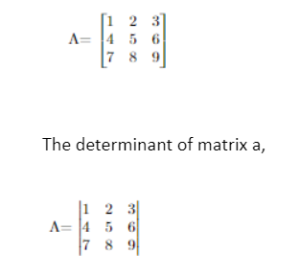
How to Find Determinant of Different Order Matrices 

Determinant of 1 X 1 matrix 

The matrix of order 1 x 1 has only one number and the determinant of the 1 x 1 matrix is the number itself.

Determinant Of 2 x 2 Matrix 

For the matrix of order 2 x 2, we have two rows and two columns. The determinant of matrix 2 x 2 can be find out as follows: Let us consider a matrix,

Its determinant is given by |A|,              

Determinant of 3 x 3 Matrix 

To find the determinant of a 3×3 matrix, we can expand the determinant along its rows or columns. There are a total six ways of expanding a determinant corresponding to each of three rows and three columns.

Let us understand how to find the determinant of a 3 x 3 matrix. 

Expansion along row 1 

Consider a matrix 

         Determinant Of 4 x 4 Matrix 

As we have seen in 3×3 determinants, the same pattern follows for 4×4 determinants. Let’s understand the steps to calculate the 4 x 4 matrix.

 Properties Of Determinants

Let us discuss some of the important properties of determinants.

1. In any square matrix A, if any row or column is multiplied by some constant C, then |A’| = C|A|.
2. For an identity matrix, the determinant is 1.
3. If each element of the matrix is zero, then its determinant is equal to zero.
4. If there is any zero row or zero column, the determinant is equal to zero. 
5. If two any two rows or columns are equal or proportional, then the value of the determinant is zero.
6. Interchanging the rows or columns will change the sign of the determinant; however, the value remains the same.
7. The transpose of the matrix does not change the value of the determinant. Thus, for a matrix A |AT| = |A| .
8. For any square matrix, say A, the inverse is given by A-1. Then the value of |A-1| = 1|A|.
9. In a triangular matrix (upper triangular matrix or lower triangular matrix), the determinant is given by the product of its diagonal element.

Conclusion 

We have learned about determinants, which is the scalar value that exists for a square matrix. The determinant of a matrix helps us to find whether the square matrix is invertible or not, to find the cross product of the vectors. The value of the determinant can be found out by expanding the determinants using some basic rules and formulas. The operations on determinants can be performed by using the properties of the determinants. These properties help us to simplify the determinants more easily.