A matrix is an n × n matrix. That’s a matrix having the identical number of rows as columns. For instance, the subsequent matrices are square: 

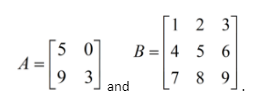
A unit matrix could be a square matrix with all diagonal entries adequate to 1.

Definition of Matrix

An n × n matrix is claimed to be a matrix of order n. In other words, when the number of rows and also the number of columns within the matrix match,  then the matrix is called a square matrix.

Determinant of a Matrix

The determinant of a matrix can be found in diverse ways. First, we have to interrupt the given matrix into 2 x 2 determinants so that it will be easy to search the determinant for a 3 by 3 matrix.

Square Matrix of Order 2

The matrix of order 2 is the matrix with two rows and a pair of columns.

Determinant Of 2 x 2 Matrix 

For the matrix of order 2 x 2, we have two rows and two columns. The determinant of matrix 2 x 2 can be found as follows: Let us consider a matrix,

Square Matrix of Order 3

A matrix of order 3 contains three rows and three columns, which means its order is 3×3.

To Find Determinant of 3 x 3 Matrix 

To find the determinant of a 3×3 matrix, we can expand the determinant along its rows or columns. There are a total of six ways of expanding a determinant corresponding to each of three rows and three columns.

Let us understand how to find the determinant of a 3 x 3 matrix. 

Expansion along row 1 

Consider a matrix 

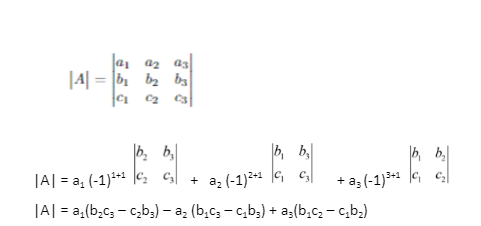
Note: To expand the matrix along columns, we will follow the same steps but instead of a1 , a2 and a3, we will expand it along the columns (a1 , b1  and c3). 

Example: Calculate the value of a given  3 x 3 determinant.

Square Matrix Determinant

The determinant of a matrix is the scalar value or variety estimated by employing a matrix. The matrix may well be any number of rows and columns like 2×2, 3×3, 4×4, or within the type of n × n, where the number of columns and rows are equal.

A determinant may be an imaginary number related to every matrix. 

Properties of Determinants

Let us discuss some of the important properties of determinants.

  1. In any square matrix A, if any row or column is multiplied by some constant C, then |A’| = C|A|.
  2. For an identity matrix, the determinant is 1.
  3. If each element of the matrix is zero, then its determinant is equal to zero.
  4. If there is any zero rows or zero columns, the determinant is equal to zero. 
  5. If any two rows or columns are equal or proportional, then the value of the determinant is zero.
  6. Interchanging the rows or columns will change the sign of the determinant; however, the value remains the same.
  7. The transpose of the matrix does not change the value of the determinant. Thus, for a matrix A, |AT| = |A| .
  8. For any square matrix, say A, the inverse is given by A-1. Then the value of |A-1| = 1|A|.
  9. In a triangular matrix (upper triangular matrix or lower triangular matrix), the determinant is given by the product of its diagonal element.

Square Matrix Properties

A number of the essential features of rectangular matrices are mentioned below:

1) The number of rows and columns is equal.

2) The sum of all the diagonal elements of a matrix is termed the trace of a matrix. If all the diagonal elements of a matrix are capable of 1, then it’s called a unit matrix.

3) For a matrix, we are able to perform different operations like the inverse provided its determinant is not 0.

4) The determinant value is often calculated just for the matrix.

5) The order of transposition of a matrix is the same because of the original matrix.

Conclusion

The matrix may be a Latin word that suggests something is created or produced. It is a useful and powerful tool for mathematical analysis and collecting data. The amount comprising the array is called elements of the matrix. The quantities m and n are known as dimensions of the matrix.A square matrix is a matrix with equal number of rows and column.We learnt about various properties of square matrix and its determinant and how to calculate it etc.