When we write y=sin𝜽, we express the sine as a function of the angle denoted by 𝜽. This means that the angle is the independent variable and the sine is the dependent variable.
However, we may require to reverse this relation; i.e. to express the angle as a function of the sine. The sine then becomes the independent variable and the angle the dependent variable. This expression is written as
𝜽=sin-1y or arc siny
Which means “𝜽” is the angle of which y is the sine.
With this, we shall note the following;
1.If x=siny, the inverse function is
𝜽=sin-1y or arc siny
2. The domain of definition of sin-1y is -1≤x≤1. That is the range of siny. The range of arc sinx is the set of real numbers.
3. This inverse function is a valued function, i.e. for any assigned value of x, there is an infinite number of values of y, whereas, y=sin x is a single valued function.
4. All the other trigonometric functions can similarly be expressed as inverse functions.
Now derive the formula for finding their differential coefficients.
Differentiation of sin-1x and cox-1x
Let y=sin-1x
Then,
x=siny
Differentiating x with respect to y
dx/dy=cosy
∴dy/dx=1/cosy
Using the relation
sin2x+cos2y=1, we have cosy=√1-sin2y=√1-x2
Hence, we have
dy/dx=1/√1-x2
Similarly,
if y=cos-1x
Then, dy/dx=-1/√1-x2
Differentiation of tan-1x and cot-1x
Let y=tan-1x
Then
x=tan y
Differentiating x with respect to y,
dx/dy=sec2y
∴dy/dx=1/sec2y=1/1+tan2y=1/1+x2
I.e. dy/dx=1/1+x2
Similarly,
if y=cot-1x
dy/dx=-1/1+x2
Derivative of Inverse Function
Let l=f(x), then x=f-1(y)
Put f-1(y)=g(y)
∴x=g(y)
∴d/dx[x]=d/dx[g(y)]dydx
1=dx/dy.dydx
∴1/dx/dy=dy/dx
Or dy/dx=1/dx/dy
Example:
If y=3√x, find dx/dy
Solution:
Method 1
y=x1/3
dy/dx=1/3x-2/3
dy/dx=1/3(3√x)2
∴dx/dy=1/dy/dx=3(3√x)2
dxdy=3y2
Method 2
y=3√x
y3=x
x=y3
dx/dy=3y2
Conclusion
To summarise, we have the following:
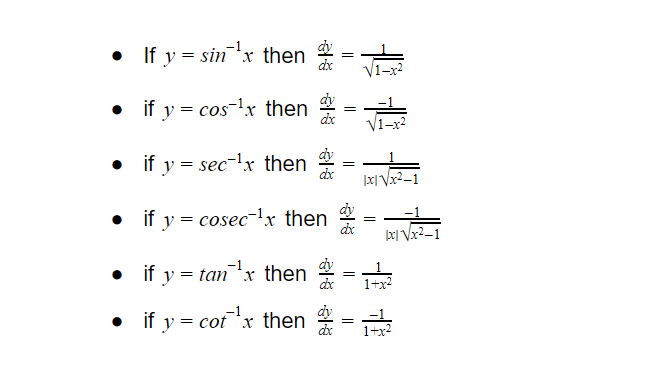
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






