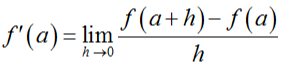Derivability and Derivative of Functions

A differentiable function of one real variable is one whose derivative occurs at each point in its domain, according to mathematics. In other words, each interior point in the domain of a differentiable function has a non-vertical tangent line on its graph. A continuous function is a differentiable function (at every point where it is differentiable). If its derivative is likewise a continuous function, it is continuously differentiable.

Most functions encountered in practice have derivatives at all or almost all points. However, Stefan Banach’s conclusion asserts that in the space of all continuous functions, the set of functions that have a derivative at some point is a small set.

What is Differentiable?

If the derivative of a function exists at all locations in its domain, it is said to be differentiable. If a function f(x) can be differentiated at x = a, then f′(a) exists in the domain. 

The definition of differentiability is expressed as follows:

• f is differentiable on an open interval (a,b) if lim h→0 f(c+h)-f(c)h
• exists for every c in (a,b).
• f is differentiable, meaning  f’(C)exists, then f is continuous at c.

Rules for Differentiable Functions

If g and f are differentiable functions, we may compute the derivatives of their quotient, difference, sum, and product using some rules. Here are various differentiability formulas for finding a differentiable function’s derivatives:

• (f + g)’ = f’ + g’
• (f – g)’ = f’ – g’
• (fg)’ = f’g + fg’
• (f/g)’ = (f’g – fg’)/f2

Derivatives as linear approximations. 

f(c + h) = f(c) + f 0 (c)h + r(h) can also be written as the sum of a linear (or, scientifically yes, affine) approximation f(c) + f 0 (c)h of f(c + h) and a remainder r. (h). The remainder is likewise dependent on c in general, but we don’t indicate this clearly since we consider c to be fixed.

A differentiable function with discontinuous partial derivatives

In order for a function to be differentiable, the differentiability theorem stipulates that its continuous partial derivatives must be present. It’s crucial to note, however, that the differentiability theorem prevents you from drawing any conclusions simply because a function has discontinuous partial derivatives. The opposite of the differentiability theorem is false. Discontinuous partial derivatives are conceivable for a differentiable function.

The chain rule

The composite of differentiable functions is differentiable, according to the chain rule. If one thinks of derivatives as linear maps, the outcome is pretty intuitive. The chain rule is usually the sole technique to distinguish a composite function. We won’t be able to differentiate correctly if we don’t realize that a function is composite and that the chain rule must be applied. Applying the chain rule to a non-composite function, on the other hand, will likewise result in an incorrect derivative.

The derivative of a function at a particular location, as we’ve seen, tells us the growth rate or slope of the line segment to that function. We can get the velocity at a particular moment by differentiating a position function at that time. It is logical to assume that knowing the function’s derivative at each point would provide useful information about the function’s behavior.

Points to remember

Functions that have derivatives are referred to as differentiable functions.

• If a function can be differentiated, it can also be continuous.
• If a function is continuous, it does not always have to be differentiable.
• There are no breaks, corners, or cusps on the graph of a differentiable function.

Conclusion

In this article, we studied the derivability and derivative of Functions.  In calculus, a differentiable function is a one-variable function whose derivative occurs at every point in its domain. At each interior point in a differentiable function’s domain, the tangent line to the graph is always non-vertical. As we’ve seen, the rate of change or slope of the tangent line to a function at a particular location is determined by the derivative of that function. In order to acquire the velocity at a specific time, we must distinguish a position function at that time. It is fair to assume that knowing the function’s derivative at each point would provide valuable knowledge about the function’s behavior. You can use a partial derivative calculator or second derivative calculator available online for your convenience.