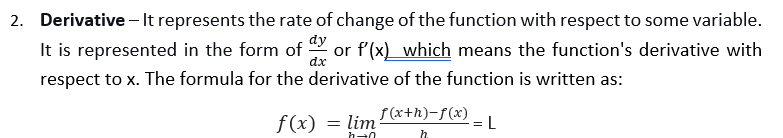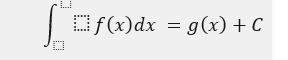Calculus

Calculus is the field of mathematical study that deals with the study of change. It is the Latin word that means ‘small pebble’. In ancient Rome, pebbles were used for counting the distance traveled by a vehicle, and the word usually means the method of computation. It is the mathematical study of continuous change, which can be called the “calculus of Infinitesimals”. In this article, we will learn about the definition of calculus, the basics of calculus, and the types of calculus.

Definition Of Calculus 

Calculus is a field of mathematics that deals with the study of change. It is used for understanding the change between the values related to the function and thus helps us to find an optimal solution. It is broadly classified into two categories which are’ Differential Calculus ‘and ‘Integral Calculus ‘.

Basics Of Calculus 

Calculus deals with the study of differentiation and integration. Differential calculus deals with the rate of change, slopes, and finding the maximum and minimum value of the functions. Whereas integral calculus deals with the areas under and between the curves. Apart from this, concepts like continuity exponents are part of the advanced form of calculus. 

Types of calculus 

Calculus can be classified into various forms; however, in this article, we will learn about the two main branches of calculus, Differential calculus, and Integral calculus.

Differential calculus 

Differential calculus deals with the problems related to the rate of change of a function to find the maxima and minima values of a function. ‘dy and ‘dx’ represent the small change in the value of the variable and are known as differentials. The function’s derivative is represented by dy/dx, which means the derivative of y with respect to x. The following subjects come under differential calculus.

1. Limits – As the value of x approaches the input value, the function’s value gets closer to the value of the output. It is essential for calculus and mathematical analysis. It is defined as f(x) =L, which means that as x approaches a the value of the function f(x) approaches L.

4.Integral Calculus

Integral calculus is used to examine the total size or value, such as lengths, areas, and volumes of curves or surfaces. It is the branch of calculus where we study the accumulation of quantities and the areas under and between curves. The method of finding the integral is called integration. It is the reciprocal of the differentiation. Integration can be understood as the sum of small parts to form a whole part. The integrals can be defined as follows:

1. Definite Integrals – Definite integrals are defined over specific limits and boundaries. The upper and lower limit of the function is always given. The definite integrals have a constant limit. It is represented as 

1. Indefinite Integrals – The indefinite integrals are not defined over some specific boundary. The upper and lower limit of the function is not given. In Indefinite integral, it is mandatory to add some arbitrary constant after calculating the integral of the function. it is represented as:

Applications Of Calculus 

Calculus is a very versatile tool in mathematics. It is used in real-life applications like finding the area of complicated shapes, economists use it to evaluate changes in conditions of a system, for analyzing the data in business planning. Also, used by architects for designing bridges, buildings, etc. Calculus helps us analyze how particles, stars, and matter move and change in real-time.

Conclusion

Calculus is a mathematical tool used to analyze the study of continuous change. It has two major branches which are differential calculus and integral calculus. The differential calculus is used to find the rate of change and maxima and minima values of the function. The integral calculus is majorly used to find the areas under the curves. Calculus has many real-life applications like calculating the areas of complex shapes, designing buildings, and analyzing business behaviors.