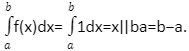Area Between Two Curves

The area is a volume in 2D geometry that describes the region inhabited by a two-dimensional figure. We can use an integral calculation to determine how much area lies between two intersecting curves. We can use integral calculus to calculate the area between two curves, when we know the equation of the two curves and the places at which the two curves cross.

The simplest approach to finding the area between two curves is to divide the area beneath the higher curve by the area beneath the lower curve. Then, we need to find the differences between the two functions’ definite integrals to find the area between two curves. 

How To Find the Area Between Two Curves?

To find the area, you will need two functions, say f(x) and g(x), as well as the integral limits of the function from ‘a’ to ‘b’ (b should be >a) and the shape of the curve. When these two functions meet, the area between them is defined as the difference between their respective definite integrals (a/b). We can calculate this difference by subtracting f(x) from its opposite g(x). We can express this definition in algebraic form as follows:

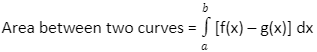
The upper function, f(x), is assumed to be the function with the higher value of y for a given x. On the other hand, the lower function, g(x), is taken to be the function with the smaller value of y for a given x.(x)

Similarly, the right function, u(y), is defined as the function with the bigger x value for a given y, whereas the left function, v(y), is defined as the function with the smaller x value for a given y. (y). These functions vary depending on the graph’s distinct sections. In such instances, we must determine the area of each zone separately.

The following is the fundamental mathematical expression for computing the area between two curves:

• If x₁ and x₂ are the two limits, and P: y = f(x) and Q: y = g(x),

• Now use the conventional formula: A=x₂x₁f(x)g for the area between two curves (x)

You should be able to do the following with this topic:

• Calculate the distance between two curves

• Integrate two curves to determine the area between them

Examples of The Area Between Two Curves

Consider the following scenario for a better understanding:

Calculate the region’s size delimited by y =2x2+10and y=4x+16.

Solution:

2x2+10=4x+16

2x2−4x−6=0

2(x+1)(x−3)=0

two curves will intersect at x=−1 and x=3.

A=∫ba( upper function )−(lower function)dx

= ∫3−1 4x+16−(2x2+10)dx

=∫3−1−2x2+4x+6dx

=64/3

How to Find Area Under The Curve?

Three simple procedures may be used to compute the area under the curve. To begin, we must understand the curve’s equation (y = f(x)), the constraints within which the area must be determined, and the axis encompassing the area. Second, we must determine the curve’s integration (antiderivative). Finally, we need to take the difference between the integral solution and the upper and lower limits to get the area under the curve.

Follow the procedures below to compute the area under a curve f(x):

• Shade the region

• Determine the a and b limits.

• Determine the absolute value of the definite integral

• Carry out the integration

The shaded region represents the area between two curves. We can easily calculate it from the difference of the definite integrals for the upper and lower curves. There are two cases for finding the shaded region between two curves:  

• When you have only one function 

• When you have two functions at once

Calculating the Area Between Curves Using Double Integrals

We can compute the area under a curve f(x) across certain intervals a, b using the single variable integral by integrating f(x) over that interval. We can also use double integrals to determine the area between the curves on occasion. 

The length of the interval a, b is the integral of the function f(x) =1. It may also be defined as the area of a rectangle with height 1 and length (ba), but we can alternatively define it as the length of the interval a, b.

Conclusion

This article discusses how to calculate the area between two curves. Based on the examples, we can achieve the values for an area between two curves by finding the area bounded by one of these curves and a line. 

Geometrically, the area between two curves is the region under one of these lines. The calculations of this field are the same as those in other areas in geometry, but they are more complicated.