Adjoint and Inverse of a Matrix

What is the Inverse Matrix?

When two matrices are multiplied together, the inverse of a matrix is described as the identity matrix. As a result, if AB = BA = I, B is the inverse matrix of A, and A is the inverse matrix of B by definition. So, if we consider B = A-1, then AA^-1 = A^-1A = I

Definition: Inverse of a Matrix

Let 𝐴 be an 𝑛×𝑛 matrix. The inverse of 𝐴 (denoted by 𝐴) is an 𝑛×𝑛 matrix that satisfies 𝐴𝐴-1=𝐼, where 𝐼 is the 𝑛×𝑛 identity matrix. If such a matrix exists, we say that matrix 𝐴 is invertible.

Although this extension is feasible, deriving formulae for such matrices, or even knowing if they exist in the first place, is simpler said than done. We may get the inverse in the instance of 22 by manipulating the matrix elements and dividing by the determinant, assuming it is not equal to zero. We could question if a similar technique exists for scenarios with more dimensions.

The fact that the determinant of A is not zero is a necessary and sufficient condition for a matrix to be invertible. In other words, |A| = det(A) ≠ 0. If a matrix meets this criterion, it is said to be non-singular,  invertible, or non–degenerative. As a result, A is a square matrix, and 𝐴-1 and A are of equal size.

The adjoint may be used to discover the derivative of a determinant using Jacobi’s theorem and to compute the inverse of a matrix. The word “adjoint” has fallen out of favor and is now reserved for a matrix’s complex conjugate. As a result, the adjugate matrix or adjunct matrix is the right phrase.

Formula: Inverse of a 2 × 2 Matrix

Let 𝐴=

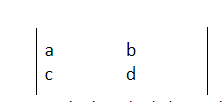
such that det(𝐴)≠0, where det(𝐴)=𝑎𝑑−𝑏𝑐 is the determinant of 𝐴. Then the inverse of 𝐴 is given by𝐴-1=

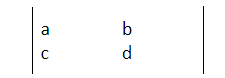
/det(A)

If det(𝐴)=0,matrix 𝐴 is not invertible.

Note: For inverse of a matrix to exist:

The given matrix should be a square matrix.

The determinant of the matrix should not be equal to zero.

What is the difference between Inverse and Adjoint  Matrices?

• The transpose of the cofactor matrix is the adjugate or adjoint of a matrix, whereas the inverse matrix is a matrix that when multiplied together provides the identity matrix.

• The adjugate matrix is one of the most frequent techniques of manually determining the inverses and may be used to calculate the inverse matrix.

• An adjugate matrix exists for any matrix, but if the determinant is non-zero, then only the inverse would exist.

What is the Adjoint and adjoint of a matrix formula?

The matrix formed by transposing the cofactor matrix of a particular square matrix is termed the Adjoint (or Adjugate) matrix. Adj is the Adjoint of any square matrix ‘A’ (for example) (A).

Obtaining the transpose of the matrix’s cofactor members yields the adjoint of a matrix. The adjoint of a matrix is one of the most basic ways for computing the inverse of a matrix. The transpose of the matrix [Aij ]nxn where Aij is the cofactor of the element aij, is defined as the adjoint of a square matrix A = [aij ]nxn. adj A denotes the joining of the matrix A.

finding the Adjoint Matrix of a 3 × 3 Matrix

Answer

Remember that the adjoint matrix is the transpose of the cofactor matrix, which would be a matrix in which each entry is a cofactor of the element to which it corresponds. Let A be the provided matrix.

To get the minors of A, we must first discover the minors, which may be done by taking each element of the matrix one at a time, eliminating the rows and columns to which they belong, and then taking the determinants of the remaining 2×2 matrices.

Finding the Inverse of a Matrix with Variable Entries Using the adjoint of a matrix formula

Answer

We don’t need to examine whether the determinant is nonzero in this issue since it’s assumed that the supplied matrix is invertible. However, in order to obtain the inverse, the determinant must be calculated, Assume A-1=adj(A)/det(A), where det(A) is the determinant and adj(A) is the adjoint matrix (i.e., the transpose of the cofactor matrix). Let A be the provided matrix.Normally, manipulating the matrix such that two of the three elements in a single row or column are 0 is advantageous. This indicates that only a single cofactor is required.

Conclusion

In this article, we have gone through various details of the Adjoint and Inverse of a Matrix. For matrix A, the inverse of the Matrix is 𝐴-1. A simple formula may be used to determine the inverse of a 2 x 2 matrix. In addition, we must know the determinant and adjoint of a 3 x 3 matrix in order to compute its inverse.