De Broglie’s Theory

Introduction

De Broglie’s theory is the one of the most fundamental theories which gives a direction to quantum mechanics from  classical physics. It describes the dual nature of matter, i.e., a matter can behave like both particle and wave.  The phenomenon of a beam of light which diffracted just like a wave is explained by this theory.

In 1924 a French physicist, Louis de Brogile gave the proposal about the wave nature of the particle.It was observed that the electron which we usually think of as a particle may in some situations behave like a wave.

Body

Observing the wave nature of the electron :

De Broglie’s proposal of De Broglie’s theory was a bold one, made at the time when there was no direct experimental evidence that particles have wave characteristics. But within a few years his ideas were verified by diffraction experiments. There are also some other experiments like three dimensional diffraction grating by X ray, Bell Telephone Laboratories experiment and others like these which prove the wave nature of the microscopic particle which is in motion. 

Electron Waves And The De Broglie’s Theory  :

If a particle acts as a wave, it should have a wavelength and a frequency. According to De Broglie’s theory free particle with rest mass m, moving with non-relativistic speed v, should have a wavelength related to its momentum p=mv in exactly the same way as for a photon, as expressed by the equation:

If the de Broglie picture is correct and matter has wave-like aspects, you might wonder why we don’t see these aspects in everyday life. As an example, we know that waves diffract through a single slit. Yet when we walk through a doorway (A kind of a single slit), we dont worry about our body diffracting!

The main reason we don’t see these effects on human scales is that Planck’s constant h has such a minuscule value. As a result, the de Broglie wavelengths of even the smallest ordinary objects that you can see are extremely small, and the wave effects are unimportant. For instance, what is the wavelength of a falling grain of sand? If the grain’s mass is 510-10 kg and its diameter is 0.07mm = 710-5 m, it will fall in air with a terminal speed of about 0.4 m/s. The magnitude of its momentum is p = mv =(510-10)(0.4m/s)= 210-10kg.m/s. Now if we calculate the wavelength then it will be

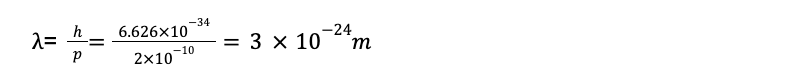
So this wavelength is very small, that’s why we cannot observe this in our real life. 

A more massive and high moving body has more momentum and even smaller de broglie wavelength.The effect of such tiny wavelengths are so small that they are never noticed in our daily life.

Application Of the  De Broglie’s theory :

1.Electron microscope 

An electron microscope offers an important and interesting example of the dual nature of electrons. An electron beam can be used to form an Image of an object much similar to that of light. So here the wave nature of the electron comes into the picture for image formation. 

Which is an application of  De Broglie’s theory.

2.Atomic Spectra 

Every neutral atom consists of at least one electron.  So when a material is heated it emits light, and different materials have different types of the light. This is because of the dual nature of the matter.Again which is proved by De Broglie’s theory.

3. Bohr’s Atomic Model 

According to Bohr’s Atomic Model the angular momentum of the electron is quantized.

Which proves that both Bohr’s quantization of angular momentum and De Brogliers theory are interrelated.

Conclusion 

De broglie’s theory is one of the reasons which violates the laws of classical mechanics and gives the foundation to quantum mechanics .Every particle that is moving has a wavelength associated with it which explains the dual behaviour of the matter. Various applications of this equation are well established in the field and subjects of chemistry as well as physics.