Profile
Settings
Refer your friends
Sign out
The general increase in volume of a material as its temperature rises is known as thermal expansion. A linear expansion coefficient is used to describe the expansion of a solid, but a volume expansion coefficient is more appropriate for a liquid or gas.
The expansion of a crystalline solid will be homogeneous in all dimensions if it is isometric (has the same structural structure throughout). If it’s not isometric, different crystallographic directions may have different expansion coefficients, and the crystal will change shape as the temperature varies.
Thermal Expansion
Thermal expansion happens when the temperature of a thing changes, causing it to expand and grow larger. To comprehend how this occurs, we must first consider what temperature is. The average kinetic (or movement) energy of the molecules in a substance is defined as temperature. When the temperature rises, the molecules move quicker on average.
When you heat a substance, the molecules move quicker and take up more space as a result. They tend to move into previously empty places. The object’s size grows as a result of this.
As a result, when you heat up the jar lid, it expands in the same way. Glass expands as well, but metals expand more than glass.
In General there are three types of thermal Expansion. They are as follows:
- Linear Expansion
- Area Expansion
- Volume Expansion
Volume Expansion
The increase in volume of a solid when heated is known as volume expansion. The change in volume of a solid with a change in temperature t is given by∆v= Vy∆t, where the coefficient of volume expansion is y.
When the temperature, pressure, or forces acting on a gas, solid, or liquid change, the volume of that gas, solid, or liquid changes. We’re looking at temperature-dependent changes in the instance of thermal analysis.
For isotropic materials, the volume expansion can be measured directly using a volume dilatometer or indirectly by measuring the linear thermal expansion and then computing the volume expansion using appropriate software.
The formula for temperature-dependent volume expansion is given by:
∆V=Y.VO.∆T
Here,
∆V= Volume change in m3
Y= Volumetric thermal expansions coefficient in 1/k
VO= Initial volume
∆T= Temperature change in K
We can ignore the effects of pressure on a solid and calculate the volumetric (or cubical) thermal expansion coefficient.
This signifies that a material’s volume changes by a constant fractional amount. When the temperature is raised by 50 K, a steel block with a volume of 1 cubic meter may expand to 1.002 cubic meters. This is a 0.2 percent increase.
If we had a block of steel with a volume of 2 cubic meters, it would expand to 2.004 cubic meters under the same conditions, a 0.2 percent increase. For 50 K, the volumetric expansion coefficient is 0.2 percent, or 0.004 percentK-¹.
If we already know the expansion coefficient, then
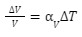
The expansion coefficient did not change when the temperature changed, and the increase in volume was minor in comparison to the original volume. This isn’t always the case, but it’s a decent approximation for small temperature changes.
Coefficient of Volume Expansion
The degree of volume expansion divided by the change in temperature is known as the coefficient of volume.
- It is symbolized by the letterav.
- It is a feature of the substance.
- It varies based on the temperature.
Conclusion
In this article we have studied thermal expansion and about volume thermal expansion. Here we have also studied the coefficient of volume expansion.
The coefficient of linear thermal expansion of a material is the ratio of strain to temperature change. The change in length of a material divided by its starting length is known as strain. As a result, the thermal expansion coefficient changes with temperature.
When the temperature of a substance rises, the intermolecular forces of that substance reduce.
