Velocity and Acceleration in Simple Harmonic Motion

Understanding Velocity and Acceleration in Simple Harmonic Motion

Simple harmonic motion is a repetitive, periodic motion. It involves back and forth movements through a central mean position or an equilibrium. This makes it such that the maximum displacement on one extreme is equal to the maximum displacement on the opposite point. The interval of time between each complete movement (i.e., from the equilibrium, then back to the equilibrium) is the same.

This motion is inflicted by a force directed to the equilibrium position. It is directly proportional to the particle’s distance from the mean position. In other words, the farther the object is from equilibrium, the higher the force it faces.

A simple harmonic motion is an instance of periodic motion. An example of this could be a body connected to a vertical spring attached to a point on the ceiling. To understand and predict the movement of an object in this motion, we must understand the equations for the position, velocity, and acceleration.

A- Acceleration and Velocity

• Acceleration is the rate of change in velocity
• Velocity is the rate of change in displacement

B- Understanding Periodic Motion and Oscillatory Motion

• The kind of motion repeated after a specific period is known as periodic motion
• An illustration of periodic motion could be a bouncing ball. At the same time, oscillatory motion involves the back and forth movement around a mean or a fixed point
• An example of oscillatory motion can be a swinging pendulum
• These two types of motion are similar, but they differ slightly
• Any oscillatory motion is a periodic motion, but any periodic motion is not oscillatory
• Unlike oscillatory motion, periodic motion does not involve a fixed or equilibrium position
• An object under periodic motion does not face a restoring force either
• An example to illustrate this can be the earth’s revolution around the sun

C. Oscillatory Motion and Simple Harmonic Motion

• Oscillatory motion and Simple Harmonic Motion are both types of periodic motion
• Oscillatory motion involves a recurrent motion variation over time between two extreme points
• In comparison, Simple Harmonic Motion is a special case of oscillations with equal changes in motion over a given period
• Simple Harmonic Motion is only theoretically feasible, whereas oscillatory motion can be present in practical conditions
• The total energy of an oscillation need not remain constant, whereas the total energy of Simple Harmonic Motion stays constant

D- Simple Harmonic Motion-Delving Deeper

• The object characterises simple Harmonic Motion in motion facing acceleration directly proportional to the displacement from its mean position
• It is considered a special case of oscillatory motion as well as periodic motion
• Displacement, force, acceleration, and velocity differ in the context of time; they are described using sine or cosine functions
• For this reason, it’s also called a Sinusoidal model
• Understanding velocity and acceleration and other relevant topics in a Simple Harmonic Motion can facilitate the study of alternating currents, sound waves, and light waves
• The object faces a restoring force directed towards the mean or equilibrium positions
• This oscillation may continue indefinitely unless it is inhibited by friction or other forces that cause energy dissipation
• Since this is impossible in realistic conditions that will cause additional effects on the velocity and acceleration, it is a perfect model

E- Spring Mass System

• The most commonly used example under this type of motion is a mass attached to one end of spring
• The spring is connected to a ceiling or some other support overhead
• When this system is left untouched, it stays in its equilibrium position
• However, when the mass moves, it applies a restorative force proportional to its distance from the equilibrium position
• This movement is illustrated using the formula

F=-kx

Solving this differential equation we get the final form of the simple harmonic motion i.e

x = A sin (ωt + Φ)

Where

A=amplitude

w= angular frequency

Φ=Phase constant

Using this we see why we get a sinusoidal graph in S.H.M.

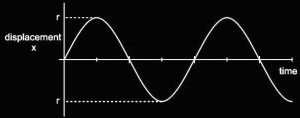
• Here, F is the restoring force wielded by the spring, k is the spring constant, and x stands for displacement from the equilibrium position
• Due to the restoring force, the spring accelerates and starts returning to the equilibrium position
• As the spring comes closer to equilibrium, the restoring force decreases, and so does the acceleration
• At the equilibrium, the total restoring force disappears. Nonetheless, at the equilibrium, the residual momentum due to the previous acceleration causes the mass to go beyond the equilibrium point
• Once again, the mass is acted upon by a restoring force which gets higher the farther the mass goes from the equilibrium
• The velocity of the object is the maximum at the equilibrium position
• As long as the spring has no energy loss, this cycle of oscillations could continue perpetually
• This is a type of Linear Simple Harmonic Motion
• The formula can give the acceleration of an object under Simple Harmonic Motion:

ω represents the particle’s angular velocity

• A formula representing the conditions required for Simple Harmonic Motion:

F=-kx

a ∝− wx (w=k/m)

F- Simple Harmonic Motion’s Two types

● Simple Harmonic Motion can be divided into two types

These types also affect the resulting velocity and acceleration.

These are Linear Simple Harmonic Motion and Angular Simple Harmonic Motion.

Linear Simple Harmonic Motion

○ This occurs when a particle moves along a straight line between two extreme points following a to and fro movement along a fixed point called the equilibrium

○ This includes the spring-mass system

○ In this type of motion, the acceleration acting on the particle or the restoring force is always proportional to the displacement

This acceleration or restoring force is always directed toward the equilibrium position

Angular Simple Harmonic Motion

• In this type of motion, the displacement of the particle is measured in terms of angular displacement
• In this, the spring factor stands for the torque constant
• The velocity and acceleration behave slightly differently in this type
• The restoring torque or angular acceleration is directly proportional to the angular displacement
• Furthermore, it is directed towards the equilibrium position

Τ ∝ θ or α ∝ θ

Where T is Torque, α is angular acceleration, and θ is the angular displacement.

Note: These two are not independent types and are analogous to each other.

G- Important words related to Simple Harmonic Motion

• Mean position: This is the point where the net force acting on a particle is zero

The restorative force acting on a particle is negative of the displacement. Therefore, this point is a stable equilibrium point.

• Amplitude: This is the greatest or the maximum displacement of a particle from its mean position
• Time Period: This is the least time taken by the particle to repeat its motion or complete one oscillation

T = 2π/ω

ω stands for angular velocity.

• Frequency: The number of oscillations per unit of time is known as frequency. Frequency=1/T 

Angular frequency ω = 2πf = 2π/T

• Phase: A vibrating particle’s state, such as its displacement and its direction of vibration at one specific instant
• The phase angle of a given particle at t=0 is considered the initial phase
• This is the angle made by the particle in a phasor diagram

We can understand the phase through the given formula:

x = A sin (ωt + Φ)

Here, (ωt + Φ) is the particle’s phase.

• Phase difference: This is the difference in total phase angles of two particles in simple harmonic motion with respect to a mean position
• When the difference between the phases of two particles in a vibrating motion is an even multiple of π, they’re considered to be in the same phase
• This can be represented as

ΔΦ = nπ where n = 0, 1, 2, 3, . . . .

 Similarly, when the difference between the phases of two particles in a vibrating motion is an odd multiple of π, they’re considered to be in an opposite phase. This can be illustrated as: ΔΦ = (2n + 1) π where n = 0, 1, 2, 3, . . . 

Conclusion

Simple Harmonic Motion is a type of oscillatory periodic motion. It involves a continuous back and forth movement around a mean position. When an object in this type of motion is away from the equilibrium, it is acted upon with a restorative force. As a result, velocity and acceleration are also affected. Simple Harmonic Motion has two types, Linear Simple Harmonic Motion, and Angular Simple Harmonic Motion. The Spring Mass System is a popular example of this motion.