Torque and Angular Momentum

Angular Momentum

The momentum that a rotating object has because of the distance between the object and the perpendicular drawn from the centre of rotation is called angular momentum. It is due to the angular momentum that you are able to paddle a bicycle without getting imbalanced. Mathematically, it is defined as the cross product between the linear momentum of an object and the distance between the object’s centre of mass and centre of rotation. This distance is equal to the radius of the circular motion of the object. Therefore, we can calculate the angular momentum of a rotating object from the below formula:

L = r*p

Here L is used to denote angular momentum, and r is the radius, i.e., distance from the axis of rotation to the object’s centre of mass. The θ is the angle between r and p where p is used to denote the linear momentum. Angular momentum is also said to be the linear momentum’s rotational analog.

Torque 

Torque is the force that accelerates the object to follow the rotational motion along its axis of rotation. Torque acts perpendicularly on the distance between the rotational axis. According to the definition of torque, it is the rate at which an object’s angular momentum changes. It is equal to the cross product between the distance from the rotational axis and the linear force acting on the object. To find the torque of a rotating object, we can utilise the below equation, i.e., equation 2:

We can use this equation to find the torque and momentum of a rotating body. Las equation can be used to find the relation between torque and angular momentum.

Newton’s Second Law in the form of angular momentum 

We can also describe Newton’s second law in the form of angular momentum. It says that if we add all the torques subjected to a particle (vector addition), it is the same as the particle’s rate of change of angular momentum. 

To understand the relationship between torque and angular momentum properly, we need to understand that two types of torques act upon a particle system. The first type is called internal torque, which is nothing but the force that the particles within the system subject on the body. The force subjected by the particles that are outside the system results in external torques.

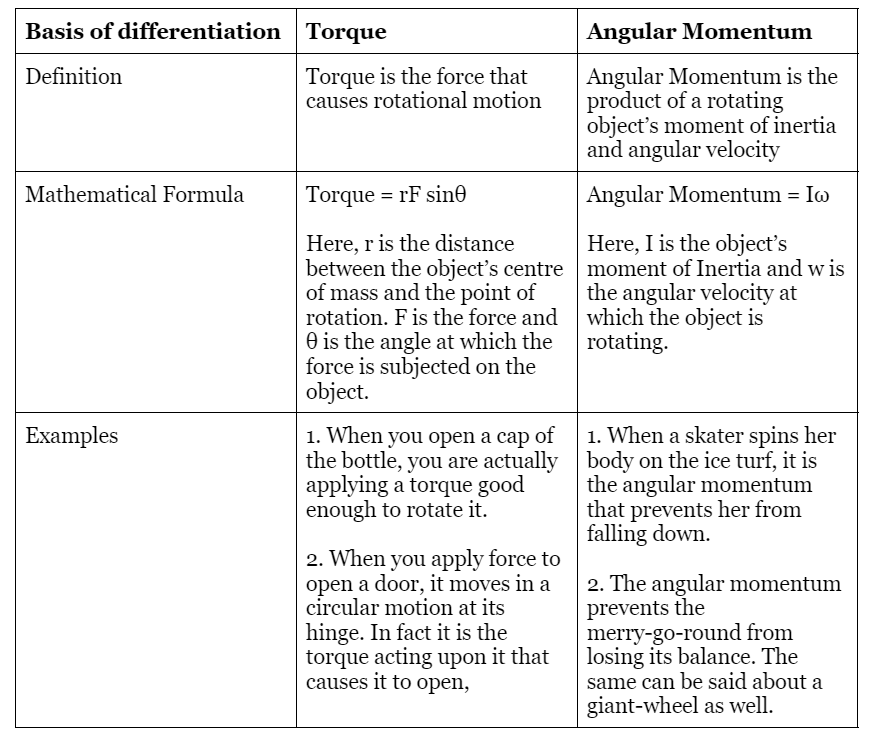
Differences between Torque and Angular Momentum

Now that we have understood the relationship between torque and angular momentum, let’s examine the differences between them. The below table shows the differences between torque and angular momentum:

Conclusion 

The above article shows the relation between Torque and Angular Momentum. Angular Momentum is the product of a rotating object’s moment of inertia and angular velocity and torque is the force that causes rotational motion. The rate of change of angular momentum is equal to the torque.