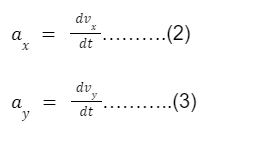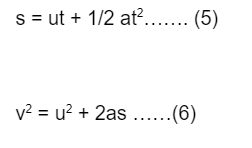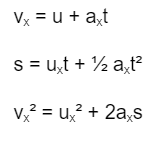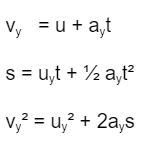Motion in a Plane

To depict the motion of an object in two dimensions (a plane) or three dimensions (space), we must use vectors to represent the physical quantities listed above. As a result, learning vectors is required first. What exactly is a vector? How do you multiply, add, and subtract vectors? This will be learned so that we can utilise vectors to define velocity and acceleration in a plane. The motion of an object in a plane is then discussed. We’ll look at motion with constant acceleration as a simple example of motion in a plane, and we’ll go over projectile motion in depth. Circular motion is a well-known type of motion that plays an essential role in everyday life. We’ll go over uniform circular motion in greater depth. In this article, we developed equations for motion in a plane that can simply be expanded to a three-dimensional example. Read this motion in a plane note carefully to understand the topic in detail.

Introduction to Plane Motion

Motion in a plane is defined as a body moving from one point to different points on the X and Y axes. The X and Y axes make up a plane, and if we measure the distance travelled along the X-axis, and the time it takes for a body to move along the vertical or Y-axis, we can calculate velocity by dividing the distance travelled by the time it takes.

Similarly, the product obtained by charting the velocity along the X-axis and the time along the Y-axis is the body’s acceleration. All motion in a plane will be discussed here, along with a complete introduction and formulas.

Motion Parameters in a Plane

We mentioned three motion characteristics in the previous heading: distance, velocity, and acceleration; in addition to these three, we have a displacement. Let’s take a closer look at the concept of motion in a plane Understanding motion in one dimension, and the following motion parameters in depth is required to comprehend motion in a plane.

Distance: It is a total body measurement that is determined from the place where an object begins its journey to the point where it ends it. We won’t know which direction we’re travelling by train because it’s a scalar physical quantity; all we’ll know is the distance we covered from Delhi to Bangalore.

Time: Because we move with the passage of time, we may use it to calculate an object’s velocity and acceleration; however, because time is a scalar variable, we only know how long it will take us to go to Delhi from Dehradun, not which direction the train will travel.

The magnitude and direction of a moving object are described by velocity, which is a physical quantity. A velocity shows how an object’s position can be described as the rate of change of its position in relation to a frame of reference and time. Well! Because velocity is the speed of an object in a specific direction, it may appear difficult.

A displacement is a physical number that specifies both the size and direction of a body’s motion; however, it is the minimum distance a body can travel in order to reach another point.

We already know that velocity is a vector quantity. Hence the magnitude of the velocity vector is determined by Pythagoras theorem:

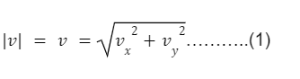
We determined the velocity along both axes and then used the Pythagoras theorem to calculate the magnitude of a velocity vector because we are discussing motion in a plane.

We have the following two equations for acceleration along both axes:

Equations of Motion in Plane v= u + at…. (4)

Let’s define equations (4), (5), and (6), which are motion in a plane formulas for a particle ‘P’ performing motion in a plane, one by one:

u represents the initial velocity.

v = maximum speed

s = particle ‘P’ displacement

t is the amount of time it takes for a particle to complete a motion.

a = the acceleration of a particle moving in a plane

The foregoing equations: (4), (5), (6) become as follows for a particle travelling along the X and Y axes:

For the X-axis, use the following formula:

The following adjustments are made to the definition:

ux denotes the initial velocity on the X-axis.

vy represents the final velocity along the X-axis.

s = particle ‘P’ displacement along the X-axis

ax = acceleration of the particle executing motion in a plane along the X-axis t = time the particle takes while executing a motion along the X-axis

Now, for Y-axis:

The following adjustments are made to the definition:

uy denotes the initial velocity on the Y-axis.

vy represents the final velocity along the Y-axis.

s = particle ‘P’ displacement along the Y-axis

ay = acceleration of the particle performing motion in a plane along the Y-axis t = time the particle takes while executing a motion along the Y-axis

Let’s look at some examples of real-world things moving on a plane:

•   Throwing a cricket ball or a cannonball are two examples of 2-D motion in a plane
•   The movement of a billiard ball and the billiard table’s floor
•   A boat moving downstream or upstream in a river
•   The Earth revolves around the Sun in a circular manner
•   A bullet’s projectile motion when fired from a gun

The Motion of a Projectile

One of the most common types of motion in a plane is projectile motion. The only acceleration acting in projectile motion is in the vertical direction, which is attributable to gravity (g). As a result, to obtain the unknown parameters, the equations of motion can be applied individually in the X-axis and the Y-axis.

A football, cricket ball, baseball, or any other object could be used as a missile. A projectile’s motion can be thought of as the consequence of two independent, concurrently occurring motion components. One component moves in a horizontal path with no acceleration, while the other moves in a vertical direction with constant acceleration due to gravity. In his dialogue on the Great World Systems, Galileo was the first to state that the horizontal and vertical components of projectile motion are independent.

Conclusion 

The motions in the x- and y-directions can be considered independently, according to one interpretation. That is, two separate contemporaneous one-dimensional motions with constant acceleration in two perpendicular directions can be considered as motion in a plane (two dimensions). This is a significant finding that can be applied to the study of two-dimensional object motion. The same holds true in three dimensions. In many physical contexts, choosing perpendicular directions is advantageous.