Simple Harmonic and Uniform Circular Motion

The study of the oscillatory system is of great importance in physics. We can describe many complex phenomena if we think of them as combinations of simple harmonic motion. One can further divide periodic motion into harmonic motion and non-harmonic motion.

We know that simple harmonic motion is the motion in which the object moves to and fro along a line. For instance, when we swing a pendulum, it moves to and fro along the same line. These movements are oscillations. The acceleration of the particle in simple harmonic motion is directly proportional to its displacement and is directed toward its mean position. The total energy of the particle that exhibits simple harmonic motion is conserved. The motion exhibits periodicity.

Definition:

Simple harmonic motion is the projection of a uniform circular motion on any diameter of the circle.

We consider a point P moving with a uniform angular velocity around a circle with a radius r and centre O.

Let PN be the perpendicular drawn from P on a fixed diameter XX’ of the circle. Then as P revolves, the foot of the perpendicular N describes a to and fro motion along the diameter XX’, with O, the centre of the circle, as its mean position.

Relating SHM and UCM:

By the time the point P completes each revolution, the point N moves from X to X’ through O, reserves its direction, and returns again to X through O. This motion of N is the SHM about O.

Point P is called a reference point, while the circle in which it moves with constant speed is called the reference circle or auxiliary circle. We may thus give an alternative description of SHM using the relation with a uniform circular motion.

Angular Frequency of SHM:

The time spent in making one complete vibration is defined as the period (T) of the particle executing SHM. It is obvious that this must be equal to the time spent by the reference point in making a complete revolution around the reference circle. Since the angular velocity of the reference point is , we have:

                                                             T=2 π/ω

If the frequency of the SHM be f, then

  n=1/ T= ω/2 π      or             ω=2πf.

is called the angular frequency of the SHM.

Displacement:

The displacement can be written as:

 x=ON=OP cos θ = r cos θ =r cos θ ωt.

The angle is described by the point P in time t. Therefore, =t

   x=r cos θ ωt.

If we reverse the direction of , then the angle () described by the point P will be the upper angle as shown in the figure. In that case,

  x=ON=OP sin θ = r sin θ =r sin θ ωt.

This is the equation of displacement of a particle executing SHM. Earlier, we obtained the same equation.

Velocity:

The linear velocity v_T of the reference point P at every instant is tangential to the circle and is given by v_T=r. Now, the motion of N at any instant is given by the component of the velocity of P along XX’.

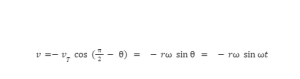
Acceleration

The acceleration (fc) of P is acting towards the centre of the circle, i.e. along PO. This acceleration is f_c=ω² r .The component of this acceleration parallel to XX’ is f=-ω² r cos θ.

Hence, the acceleration of N is

f=-ω² r cos θ = – ω²  x. 

Which is the same as the basic condition of SHM.

Conclusion:

The movement of an object going in a circular direction at a constant speed is referred to as uniform circular motion. Simple harmonic motion can be characterised as a one-dimensional projection of this motion.

Uniform circular motion occurs when a point P moves on a circular route with a constant angular velocity. Its x-axis projection is subject to simple harmonic motion. This is comparable to the linear vertical motion of an oscillating mass projected onto a spring.