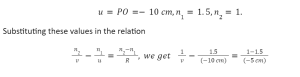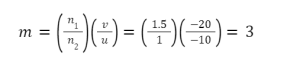Refraction is the bending of light (it also happens with sound, water and other waves) because it passes from one medium into another. The amount of bending depends on two things:
- Change in speed – if a substance causes the light to hurry up or block more, it will refract (bend) more.
- Angle of the incident ray – if the sunshine is entering the substance at a greater angle, the quantity of refraction is also more noticeable. On the other hand, if the sunshine is entering the new substance from straight on (at 90° to the surface), the sunshine will still abate. However, it will not change direction in any respect.
Refraction at a concave surface:
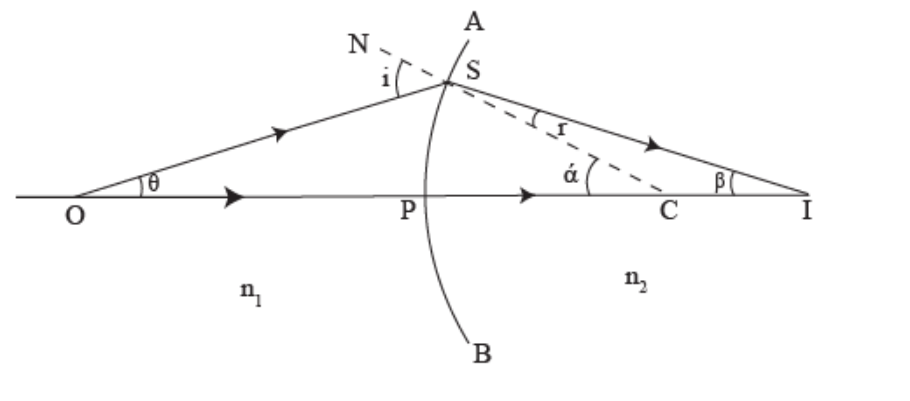
Consider a concave surface separating two media, one and two, of the refractive indices n1 and n2 (n2>n1), respectively, as shown in Figure.
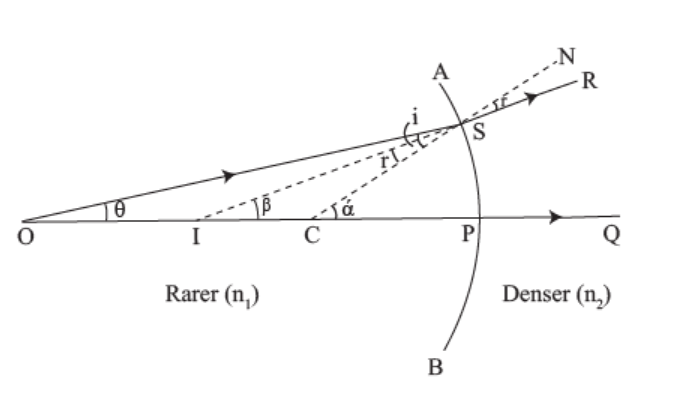
At point O, a point object is placed on the principal axis of the concave surface.
The ray OS, incident at the point S of the concave surface, travels along SR after refraction. As n2>n1, the refracted ray bends towards the normal CSN. Another ray OP, incident normally on the concave surface, is undeviated. The two refracted rays do not intersect in reality but appear to meet at point I in Medium 1.
Thus, I is the virtual image of the object placed at O.
In Figure,i=∠OSC,r=∠NSR=∠ISC,
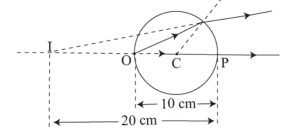
PO= object distance =-u,
PI= image distance =-v
and radius of curvature =PC=-R.
Let SCP=,∠SIP= and SOP=. Snell’s law is applied at the point of refraction S,
n1sini=n2sinr.
For paraxial rays or small aperture, i and r will be small. Hence, sinii and sinrr. Making this assumption, we can write as
n1i=n2r.
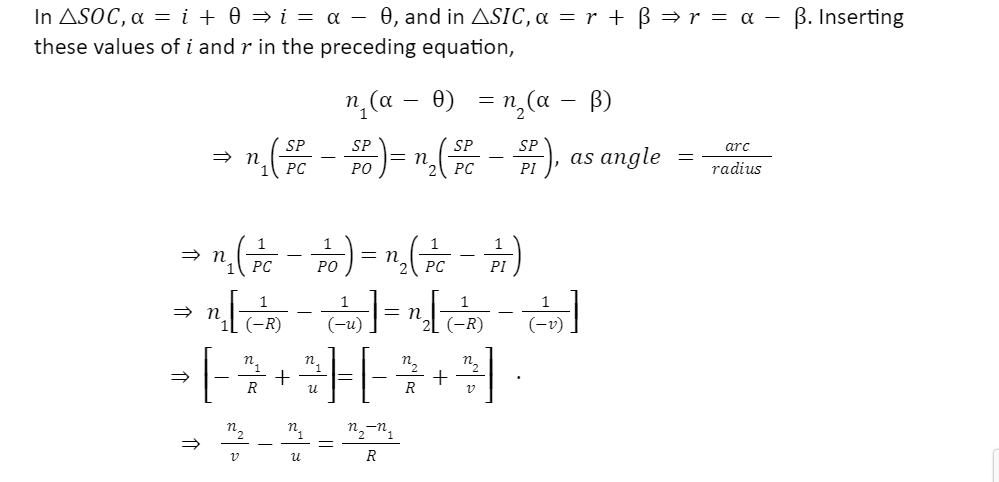
If Medium 1 be air n1=1 and Medium 2 has a refractive index n2=n, then we can write the above Equation as
n/v – 1/u = n-1 / R.
When an object is placed in the denser medium, the image of the object is formed by a concave surface dividing the two mediums. This is shown in the Figure below.
Refraction at a convex surface:
When light refracts on a convex surface, it creates a real or virtual image. We will discuss the two cases separately.
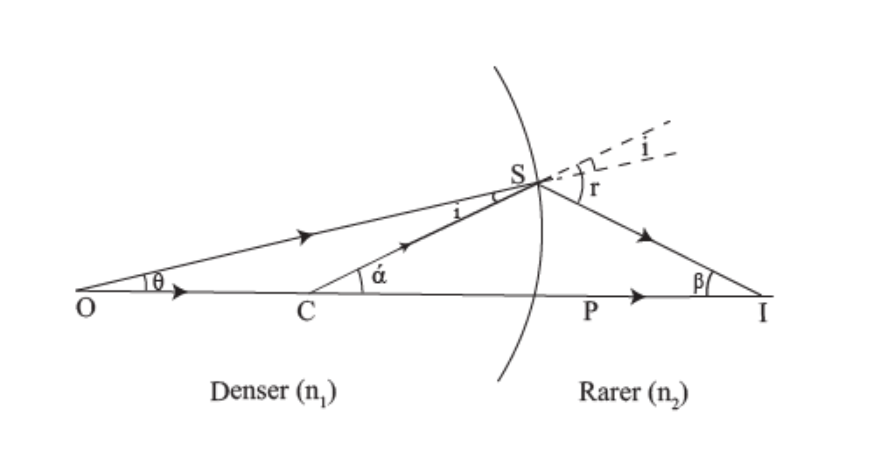
When the image is virtual: Consider a convex surface AB separating two media of refractive indices. When n2n2>n1, as shown in Figure.
P is pole, and C is the centre of curvature of the convex surface.
At the point 0, point objects are placed on the principal axis of the curved surface. The ray OS, incident at the point S on the convex surface, travels along ST after refraction.
As n2>n1, the refracted ray bends towards the Normal CSN.
Another ray OP incident, normally on the convex surface, is undeviated.
The two refracted rays do not intersect in reality but appear to meet at point I.
Thus, I is the image of the object placed at O.
OSN=i,∠CST= NSI =r
PO=-u,PI=-v ,PC=+R.
Let SCP=,∠SIP= and SOP=.
Applying Snell’s law at the point of refraction, n1sini=n2sinr.
For paraxial rays, i and r will be small. Hence, sini=i and sinr=r. Making this substitution in Equation n1sini=n2sinr.
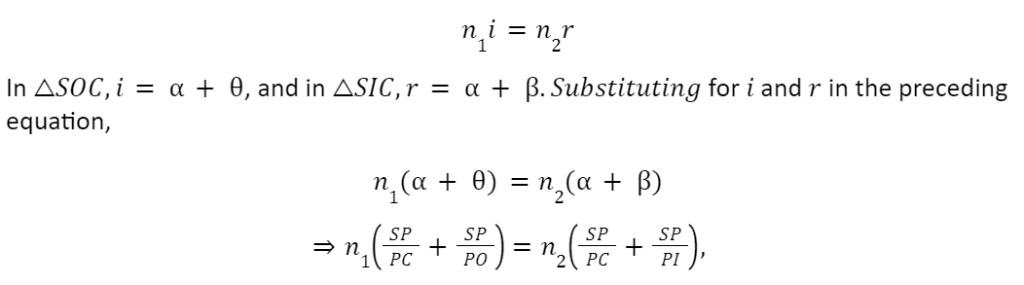

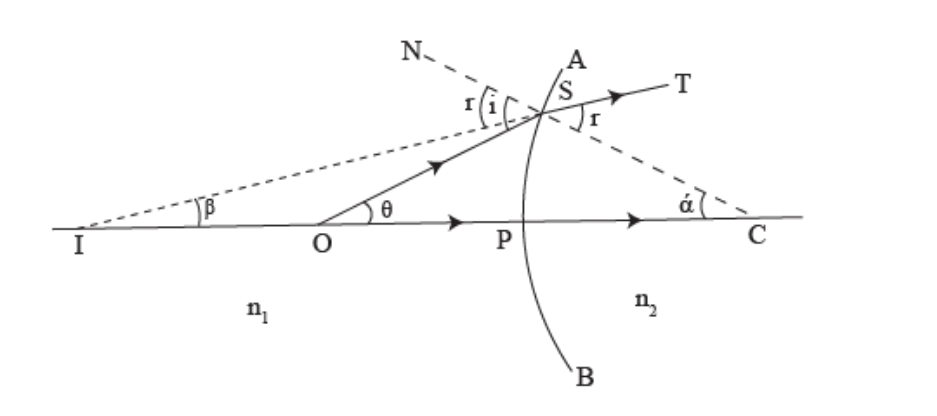
When the image is real: Consider a convex surface AB separating two media of refractive indices n1 and n2 (n2>n1), as shown in Figure.
Let P be the pole and C be the centre of curvature of the convex surface. Let a point object be placed at point O on the principal axis of the convex surface. The ray OS, incident at S, goes along SI after refraction at S. As n2>n1, the refracted ray bends towards the normal CSN. Another ray OP, undeviated. The two refracted rays intersect at I in Medium 2 . Thus, I is the real image of the object placed at O.

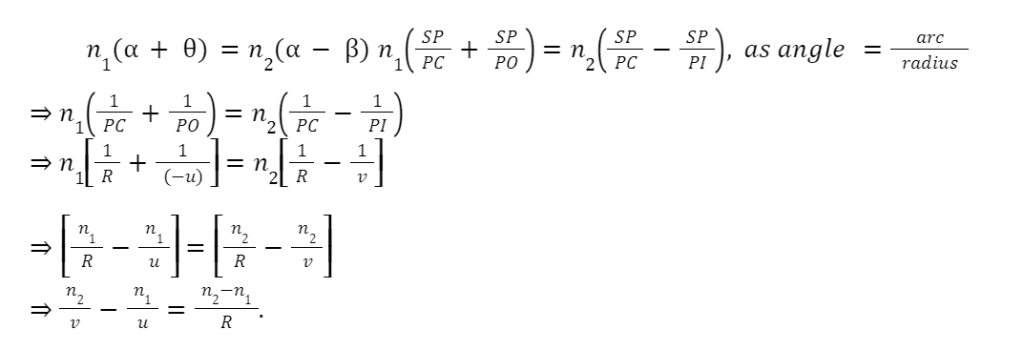
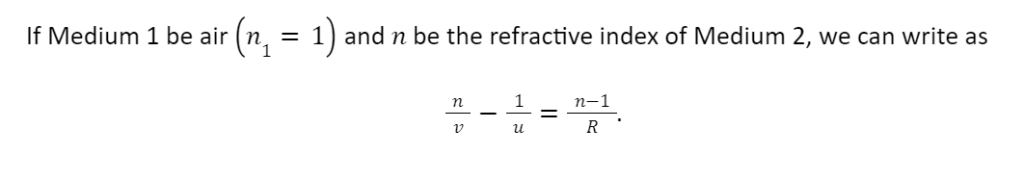
Lateral magnification:
Consider an extended object AO placed in Medium 1 (refractive index n1 ) facing a convex spherical surface MPN of Medium 2 (refractive index n2 ). Rays originating from A and O directed towards centre C will travel undeviated into Medium 2. Let the image formed be BI, as shown in Figure.
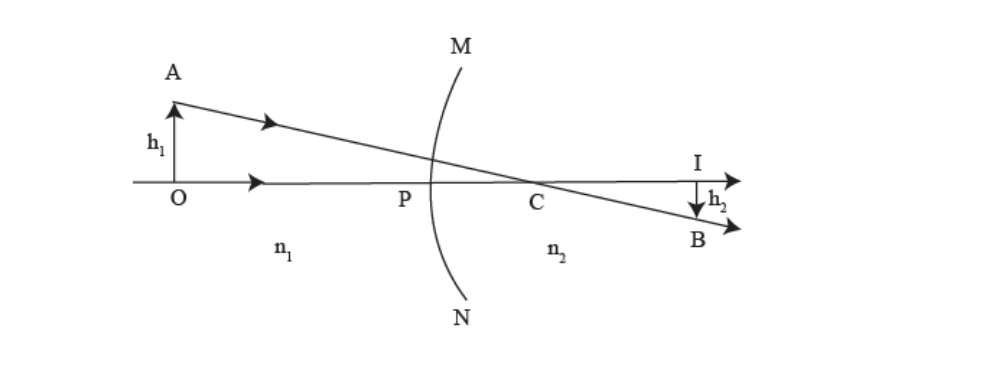
Its position may be located by using Equation

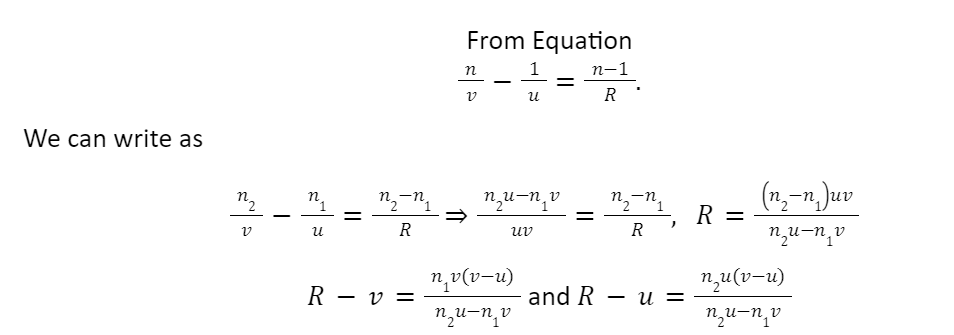
Thus,
Hence,
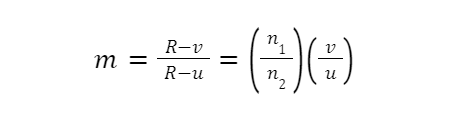
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out