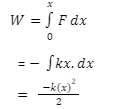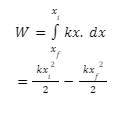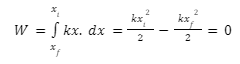Potential Energy of a Spring

The energy possessed by an object by its configuration, such as shape, size, and position, is known as potential energy. The potential energy depends on the force acting on any two things. The S.I. unit of potential energy is kg m2s-2.

For example:

• Electrical equipment until it is switched on.
• A stretched rubber band has potential energy stored in it by virtue of its shape.
• A stone kept on a table has potential energy due to its position.

Various types of Potential Energy

The various type of potential energies are as follows:

1. Gravitational Potential Energy

The energy possessed by an object by its position or when it is moved to a certain height is known as gravitational potential energy. For example- An apple hanging on a tree has gravitational potential energy.

Gravitational potential energy is calculated from the formula, E = mgh

Where,

m= mass of the object (in kilograms)

g = acceleration due to gravity

h = height from which object is thrown (in meters)

2. Elastic Potential Energy

The energy stored in an object when compressed or stretched is known as elastic potential energy. For example- An archer pulls the bow with his hand. 

Elastic potential energy is calculated from the formula, U= 12k x2

Where, 

U = Elastic Potential Energy  

k = Spring Force Constant

x = The displacement in length on the string (in meter)

3. Electrical Potential Energy

The energy possessed by two charged bodies is known as electrical potential energy. For example- the energy possessed by the electrons present in the atom of an element. 

U = q * V
Where,
U = electrical potential energy
Q = charge
V = electric potential in volts

Hooke’s Law

Robert Hooke gave the Hooke’s Law in the 17th century. Hooke discovered a direct relationship between the stress and strain of material. He found a linear region where the force applied on an object to stretch the fabric was directly proportional to the extension produced in the object. This was known as Hooke’s Law.

Hooke’s law states that “the stress applied on an object is directly proportional to the strain produced, provided stress is applied with a given elastic range of the object.”

The law can be mathematically defined as F=-kx

where, 

F is the force applied to the spring to change its position.

k is the constant of proportionality which is also known as the spring constant. 

x is a change in the position of the spring from its equilibrium position.

The negative sign in the formula represents the restoring force that always acts on the spring to restore its position. 

Potential Energy of the Spring

When you compress or stretch the string, force is experienced by the spring. When the spring is stretched, a displacement is produced in the object. The displacement in the object is responsible for the force produced in the spring. The force acting on the spring can be calculated with Hooke’s Law and helps analyse the energy stored in the spring.

Deducing an expression for the potential energy of a spring

In order to deduce the expression for the potential energy of a spring, we need to apply Hooke’s Law. The mathematical expression for Hooke’s Law is 

F=-kx

Where ‘k’ is the constant and the ‘x’ is the displacement of the object.

Suppose the block is pulled by a distance of x in the opposite direction. Now we know that work done by the spring is given by,

The work done in pulling the object is given by F= kx2 / 2

The force acting on the object is positive here as the force is required to overcome the force of the spring. Now work done by the spring is given by W= kx2 / 2

Similarly, if you displace the object by a very small distance which is tending to zero, the work done by the spring is given by W=- kx2 / 2

The work done by the force at this point is W= kx2 /2

Let the object be displaced from the initial position, say to the final position. The work done by the thing is then given by-

The expression clearly shows that the work done by the force acting on a spring depends on the displacement or the final or initial position of the object.

It is quite understood that the work done by the spring is dependent on the position of the object. In the case of cyclic motion, the work done by the spring is always zero as the work done to displace the object from the initial position ximoves back to its initial position.

Thus, work done by the spring in a cyclic process is given by

Conclusion

The potential energy of spring is zero if the process is cyclic, and it is because the net displacement in the process is zero, due to which the spring force is conservative. Thus, the spring possesses elastic potential energy because of the work done by the object.

The above study material focussed on the concept of potential energy its type and further extended the topic to the potential energy of the spring, which are essential concepts about work done by an object. These concepts will help you understand the law of conservation of energy.