Magnetic Field on the Axis of a Circular Current Loop

An electric current passing around a circular coil of wire produces a magnetic field. Magnetic field lines are formed by each short length of the current-carrying wire. Field lines become straight and perpendicular to the coil plane at the centre of the circular wire. The Biot-Savart Law can be used to calculate the magnetic field owing to a current. We start by considering arbitrary segments on opposite sides of the loop to prove qualitatively that the net magnetic field direction is along the loop’s centre axis using vector findings. The Biot-Savart Law can then be used to get the magnetic field expression.

At each point of a current-carrying circular loop, the magnetic field lines are concentric circles. The right-hand thumb rule can be used to determine the direction of the magnetic field in each portion of the circular loop. The magnetic field lines are straight at the centre of the circular loop. The magnitude of the magnetic field at a point on the coil’s axis at a distance x from its centre is given by the Biot-Savart Law.

Magnetic field due to current through a circular loop

• The field around the straight current-carrying conductor or wire is often increased by bending the wire into a circular loop.

• A circular loop is created from an outsized number of very small straight wires. A flux is produced by an electrical current flowing through the circular wire. 

• Each small section of the current-carrying wire contributes to magnetic flux lines.

• At the middle of a circular wire, field lines become straight and perpendicular to the plane of the coil. 

• The right-hand thumb rule is employed to see the direction of the field produced because of the current-carrying coil

Magnetic fIeld along the axis of circular loop 

Let’s look at how the magnetic field on the axis of a circular current loop functions. At some point, there exist two ways for calculating magnetic fields in magnetics. The Biot-Savart Law is one, and Ampere’s Law is the other. We utilise the Biot-Savart Law to compute the magnetic field of a highly symmetric structure carrying a steady current and the Ampere’s Circuital Law to estimate the magnetic field due to an infinitesimally small current-carrying wire at some point.

Use the Biot-Savart Law to determine the magnetic field produced by a tiny current element at a given place in space. We will calculate the total magnetic field owing to the circular current loop using this and the idea of superposition.

Methods for finding magnetic field 

At some point, there exist two ways for calculating magnetic fields – Biot-Savart law is one, and Ampere’s law is the other. 

Biot Savart’s Law

• Use the Biot-Savart law to determine the magnetic field produced by a tiny current element at a given place in space.

• Assume we have a finite conductor XY carrying a current I, as indicated in figure (a). The magnetic field dB owing to an infinitesimal element (dl) of the conductor must therefore be computed at a distance r from it at a point P. Assume that the angle formed by dl and the position vector (r) θ. 

• The amplitude of the magnetic field dB is proportional to the current (I), the elemental length dl, and inversely proportional to the square of the distance, according to the law. And the plane that contains dl and r is perpendicular to the direction.

• According to the law,  

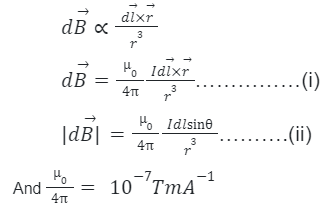
Magnetic field at current loop

• When the magnetic field created by a current-carrying piece of wire is examined, it is discovered that all segments of the loop contribute magnetic field in the same direction inside the loop.

• In a circular loop, electric current creates a magnetic field that is more concentrated in the loop’s centre than outside the loop. When numerous loops are stacked together, the field is concentrated even more into a solenoid.

Magnetic field at the centre of circular loop 

Integrating the z-component is required to apply the Biot-Savart law on the centreline of a current loop.

Conclusion 

• Magnetic field at the centre of a circular loop is a special case of magnetic field along the axis of the circular loop.

• Magnetic field in wire can be changed by bending the wire into a circular loop.

• Magnetic fields can be found by using the Biot-Savart law and Ampere Circuital law. 

• A current-carrying coil always behaves like a magnet. 

• Moving charge can create the magnetic field.

• Strength of the magnetic field is greater inside the loop as compared to outside the loop.

• Magnetic field in solenoid can be increased by increasing the number of turns.