Like scalar numbers, the vectors cannot be added algebraically. In the addition of vectors, the angle between the two vectors is crucial. When two vectors are multiplied together, the angle between them also plays a vital impact. A vector is expressed as a number with a plus (+) or minus (-) sign in front of it if it represents a quantity in one dimension—x-direction (left and right) or y-direction (up and down). The plus sign indicates pointing right or up, while the minus sign indicates pointing left or down. A vector is represented in two dimensions (x and y) by a number for magnitude and an angle for direction.
Multiplication of vector:
A vector can be multiplied by a scalar or another vector. If you multiply it by a scalar, you’ll get a new vector that’s parallel to the first and has the same magnitude as the original vector multiplied by the scalar.
- DOT PRODUCT
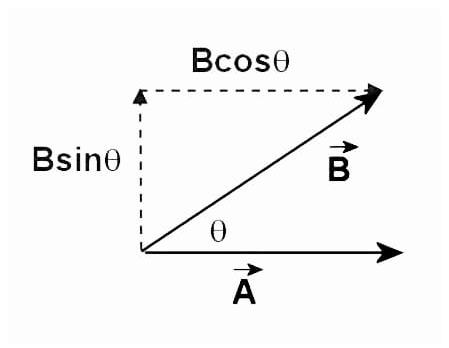
There are two methods for multiplying two vectors. The scalar or dot product is the first one. A raised dot between the two vectors is represented as A • B. There is no direction in the product; it is a scalar. The magnitude of one vector is multiplied by the parallel component of the other to get the number. That is the same as finding the product ABcos, as illustrated in Figure below.However, rather than trying to recall this formula, remember it as the product of the parallel components.
Cross product
The second type of vector multiplication yields a vector as a result and is more complicated due to the need to determine the direction of the resultant vector. The vector or cross product is a type of multiplication that is expressed as A×B The product of one vector and its perpendicular component equals the magnitude of the resultant vector. The magnitude of the product is ABsin, as shown by a vector diagram, but it is easier to remember to multiply perpendicular components than to recall this formula.The product vector will have a direction that is perpendicular to both of the original vectors. A careful examination of the scenario reveals that the two vectors A and B define a plane, and that the product vector can point in two directions, both of which are perpendicular to both vectors. It is important to employ a mnemonic device to determine the direction of the product vector. There are several of these, one of which is displayed here. Assume you’re looking for the product A×B. As shown in Figure, draw the two vectors to be multiplied so that they originate from the same location.
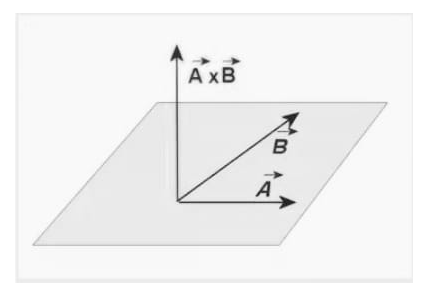
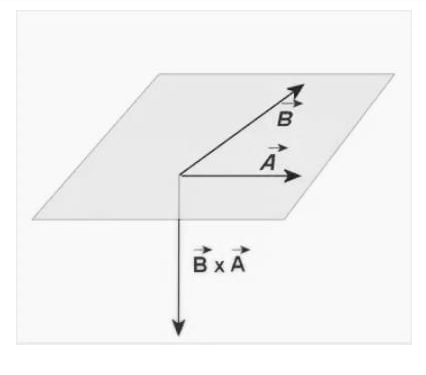
Imagine a line perpendicular to both A and B intersecting them at their point of intersection. Imagine that you’re holding that line in your right hand with your fingers wrapped around it, pointing from A to B. Your thumb is now pointing in the product vector’s direction (see above Figure). It’s important to remember that vector multiplication is not commutative. If you want to find the product B× A, your fingers must point from B to A rather than A to B, and your thumb must point in the opposite direction to do so (see Figure below).
Multiplication of vector by real numbers?
When a vector A is multiplied by a real number k, a new vector k A is created. Its magnitude increases by k times that of the specified vector. Depending on whether k is a positive real integer or not, it has the same or opposite direction as A.
Thus, n( A)=n A
And, -n( A)=-(n A)
Multiplication of vectors by a scalar?
When a vector A is multiplied by a scalar S, the result is a vector SA, whose magnitude is S times that of Aand which acts in the same direction as A. The unit of SA is not the same as the unit of vector A.
For example – if A= 100 newton due west and S=10 sec ,then SA= 10 second x 100 newton due west = 1000 newton-second due west.
Important points to remember:
A scalar quantity is the outcome of the dot product of two vectors.
The perpendicular vectors’ dot product is always zero.
The square of either vector’s magnitude is equivalent to the dot product of two comparable vectors.
A change in the order of the vectors has no effect on the dot product output.
A vector quantity is the cross product of two vectors.
In a cross product, a change in the order of the vectors leads in the introduction of a negative sign.
The cross product’s direction is always perpendicular to the plane in which two vectors intersect.
When using the right thumb rule to calculate the cross product, be sure that both vectors are pointing away from or towards the point of intersection.
When two linear vectors are cross-products, the result is always a null vector.
The magnitude of the cross-product of the two vectors equals the area of the parallelogram created by them.
Conclusion:
There are two types of vector multiplication that we have learned about. Because a vector contains both magnitude and direction, the dot product of two vectors and the cross product of two vectors are the two methods for multiplying vectors. Because the resultant value is a scalar quantity, the dot product of two vectors is also known as the scalar product. Because the output is a vector that is perpendicular to these two vectors, the cross product is termed the vector product. Aside from multiplication with real numbers, there are a few more issues worth mentioning.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






