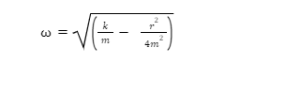Profile
Settings
Refer your friends
Sign out
Damped simple harmonic action is one type of damped oscillation. Whenever an oscillation observes uniform damping along with time, the framework would be referred to as the damped simple harmonic action. The reason behind the damping can be any external force. Moreover, damped SHM and common SHM are related to a certain extent. The angular frequency of damping is abbreviated by ‘ω’. Moreover, all damped simple harmonic actions are calculated by a formula.
Damped Oscillations
In brief, damped oscillation is an oscillating movement wherein the amplitude continuously diminishes with time. It is necessary first to understand a simple harmonic action. An oscillation where an object reflects the oscillation or moves uniformly with time can be described as simple harmonic action. Similarly, A damped simple harmonic action can be referred to as any oscillation that gets damped due to any outside force or diminishes at a uniform rate with time.
For instance, when we put a pendulum into momentum by providing its energy once, it stops after a certain amount of time because some of its power is lost in overcoming the friction of air. Thus, it loses energy continually over time. Furthermore, an RLC circuit can also be examined to understand the damped SHM.
Other types of damped oscillations
Damped simple harmonic motion is one sort of damped oscillation. There are two other types of damped oscillations, namely, over-damped oscillation and under-damped oscillations. As the terms suggest, these oscillations are excessively damped or underdamped over time.
Angular Frequency of Oscillation Formula
An angular frequency concerning a damped oscillating particle represents the damping in angle per unit time, and the angular frequency is measured on a radian scale. For example, if an entity completes an entire cycle of damping in one minute, the angular frequency of damping would be 60 radian/sec (=1 radian/min).
Moreover, the frequency is measured with one formula. First, the square root of a force constant separated by its mass equals the angular frequency conducting a common ‘simple harmonic action’. This is known as a natural angular frequency denoted by the symbol “.
Similarly, in a damped simple harmonic motion, the angular frequency is calculated by a formula of
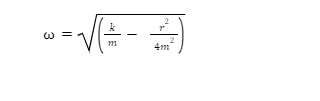
Where k depicts the spring constant, m depicts the Mass of oscillations, and r is abbreviated for the damping constant. Furthermore, this formula is used for all the damped oscillations calculations.
Forces Causing Damping Oscillations
Damped oscillations cannot take place independently. Opposite forces called damping forces are the opposing (External) forces that cause the oscillations to dampen over time. In real systems, there are numerous damping forces. However, viscous damping, Dampers and Coulomb friction are some of them, to name a few.
- Vicious damping– These forces are even weaker than the inertial and elastic pressures in most cases. Viscous damping force is a type of pressure that is impacted by velocity. Because most oscillating processes have a low velocity, the dampening pressure generated from any liquid interacting with the component is typically viscous.
- Dampers– They are devices, and these devices are implemented within the system manually to manage the vibrations of the body. These forces are relatively similar to the inertial and elastic forces in power.
- Coulomb friction damping- Coulomb damping is a constant applied to dampen actions that absorb power by friction force. Friction is a form of energy absorption caused by the relative movement of two surfaces pressing against one other. This framework is also termed as the dry friction damping.
Conclusion
We discussed various aspects of damped oscillations (and SHM). We concluded that a damped simple harmonic action is nothing but an oscillation uniformly damping (reducing) over time, unlike typical simple harmonic motion. Moreover, we also came by angular frequency of damped SHM and damping forces. The angular frequency of damped SHM is denoted by the Greek letter ‘ω’. While vicious damping, structural damping, dry damping and damping by devices are some damping forces that are the main reason behind damping oscillations.
