When light travels along the same homogeneous medium, it travels in a straight line path. However, when light passes from one medium (transparent) to another, the direction of path changes at the interface of media. This is called refraction of light.
The ray which is falling on the interface in the first medium is called an incident ray and the ray which is travelling in the second medium after being refracted is called the refracted ray.
The angle between the incident ray and the normal is the angle of incidence and the angle between the refracted ray and the normal is the angle of refraction.
It is observed that:
- The light rays bends towards the normal when they travel from a rarer medium to a denser medium.
- The light rays bend away from the normal when they travel from a denser medium to a rarer medium.
- The light rays go undeviated when they fall normally on the interface.
Laws of Refraction:
The phenomenon of refraction obeys two laws which are known as laws of refraction.
1st law : At the incident point, the incident ray, the refracted ray and the normal are always on the same plane passing through the point of incidence.
2nd law : The ratio of sine of incidence angle and the sine of refraction angle is a constant when the colour of light and two media under consideration are fixed. This constant is known as the refractive index of medium-2 with respect to medium-1.
The second law of refraction is popularly known as Snell’s law.
Let a ray of light be refracted from medium 1 to medium 2 . Angle of incidence is i
and angle of refraction is r. Then by Snell’s law sin i /sin r= 1μ2
1μ2 is a constant. It is known as the refractive index of the second medium with respect to the first medium.
Relative refractive index :
When a ray of light from the first medium is refracted into the second medium , the ratio between the sine of incidence angle to the sine of refraction angle is called the refractive index of the second medium with respect to the first medium. It is written as
1μ2= sin i/ sin r
where i= angle of incidence and r= angle of refraction.
Now, from the principle of reversibility of light path, the path of a ray of light is reversible. A ray of light travelling along BO in medium 2 will be refracted along OA in medium 1 .
Then by Snell’s law : sin i/ sin r = 1μ2
21 is called the refractive index of medium 1 with respect to medium 2.
Combining above two equations –
sin i / sin r × sin r /sin i = 1μ2 × 1μ2
=>1μ2 ×1μ2=1
=> 1μ2=1 / 1μ2
For example, refractive index of glass with respect to water wμg=9/8. So, refractive index of water with respect to glass is gμw=8/9.
Absolute refractive index :
The absolute refractive index of a medium is its refractive index with respect to vacuum. When a ray of light travels from vacuum into a medium, the value of sin isin r
is called the absolute refractive index () of the medium.
If the absolute refractive index of a medium is greater than that of another medium, then the first medium is optically denser than the second medium and the second medium is optically rarer than the first medium.
So, if 1>2, it means that the first medium is optically denser than the second medium.
Relation between refractive index and velocity of light :
The velocity of light in the medium depends on the refractive index of the medium. The absolute refractive index, μ of a media can be expressed by the following relation:
=Velocity of light in vacuum /Velocity of light in the medium=cv
If 2>1, v2<v1, then the velocity of light in denser medium is less than that in rarer medium.
(i) If velocity of light in both the media be same 12=1. Then i=r
which gives i=r. So there will be no change in direction of a ray while crossing the surface of separation and there will be no refraction,
(ii) If the medium 2 is denser, the velocity of light in it will be less and 12>1. So, i>r which gives i>r. It means the refracted ray will move towards the normal after refraction.
(iii) If the medium 2 is rarer, the velocity of light in it will be greater and 12<1 or i<r which gives i
Refraction at lenses:
- Refraction at spherical surfaces can be well demonstrated with different curved lenses.
- The axis of refraction changes on a curved surface along with the change in point of incidence.
- This is because even when the angle of incidence is the same, the normal of the surface changes at every point of incidence, as it is a curved surface.
Refraction at the Double Convex Lens:
- A double convex lens appears like two convex lenses stuck against each other at the planar side. It converges the incident light rays.
- The light rays converge at the convex surface(air to glass) like the convex lens.
- Then incidents on the second glass.
- As a concave surface, it converges the light further(glass to air)
Refraction at the Double Concave Lens:
- A double concave lens appears like two concave lenses stuck against each other at the planar side. It diverges the incident light rays.
- The light rays diverge at the concave surface(air to glass) like the concave lens.
- Then incidents on the second glass.
- It diverges the light further(glass to air) as a convex surface.
Conclusion:
In conclusion, you can mention the nature of images formed by convex lenses for various locations of objects and concave lenses. Also, with reference to the images formed you can state why a particular lens is suitable in any of the instruments like telescopes, microscope etc. You can also give examples or applications of lenses in various instruments.
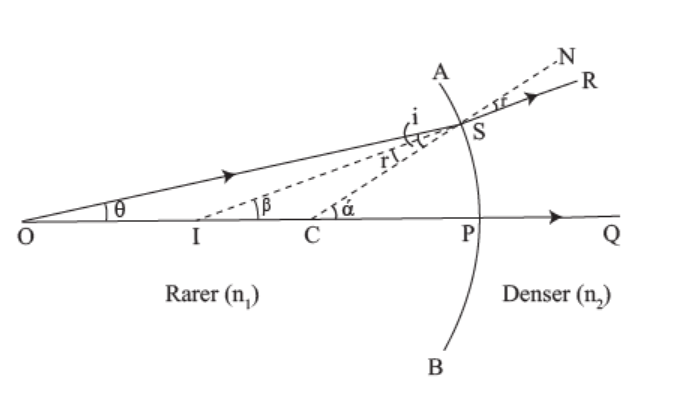
At point O, a point object is placed on the principal axis of the concave surface.
The ray OS, incident at the point S of the concave surface, travels along SR after refraction. As n2>n1, the refracted ray bends towards the normal CSN. Another ray OP, incident normally on the concave surface, is undeviated. The two refracted rays do not intersect in reality but appear to meet at point I in Medium 1.
Thus, I is the virtual image of the object placed at O.
In Figure,i=∠OSC,r=∠NSR=∠ISC,
PO= object distance =-u,
PI= image distance =-v
and radius of curvature =PC=-R.
Let SCP=,∠SIP= and SOP=. Snell’s law is applied at the point of refraction S,
n1sini=n2sinr.
For paraxial rays or small aperture, i and r will be small. Hence, sinii and sinrr. Making this assumption, we can write as
n1i=n2r.
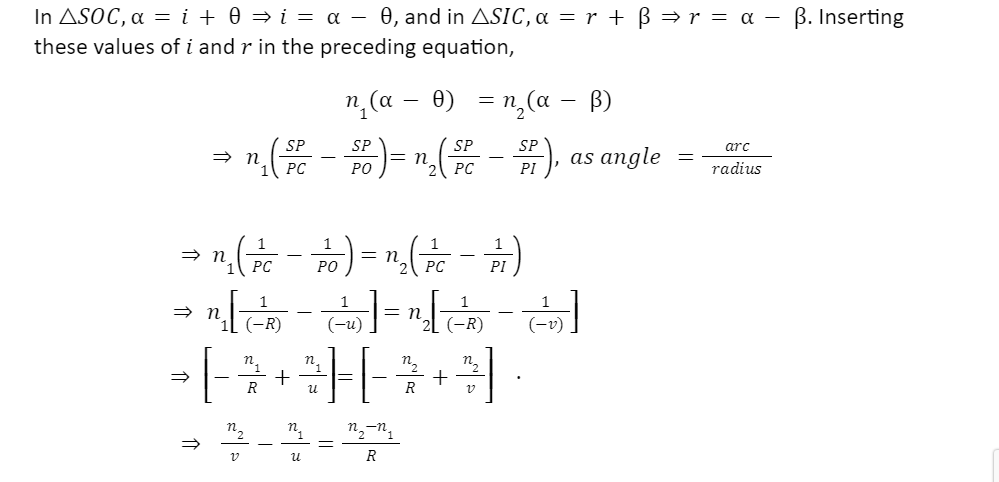
If Medium 1 be air n1=1 and Medium 2 has a refractive index n2=n, then we can write the above Equation as
n/v – 1/u = n-1 / R.
When an object is placed in the denser medium, the image of the object is formed by a concave surface dividing the two mediums. This is shown in the Figure below.
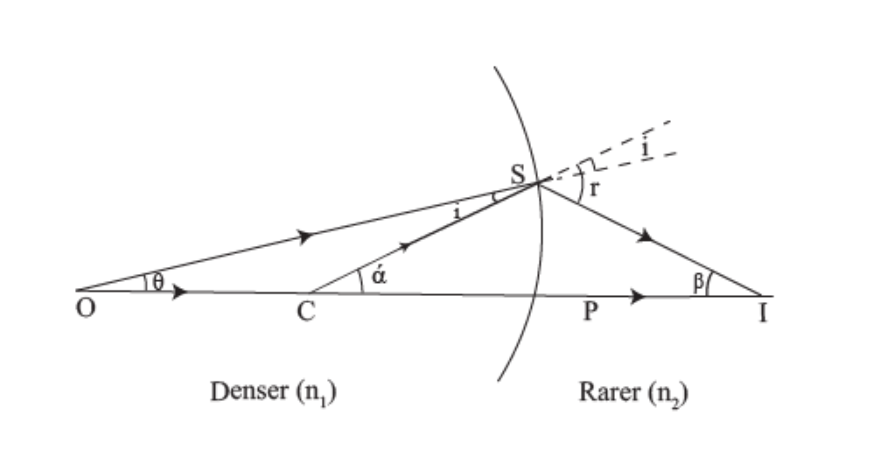
Refraction at a convex surface:
When light refracts on a convex surface, it creates a real or virtual image. We will discuss the two cases separately.
When the image is virtual: Consider a convex surface AB separating two media of refractive indices. When n2n2>n1, as shown in Figure.
P is pole, and C is the centre of curvature of the convex surface.
At the point 0, point objects are placed on the principal axis of the curved surface. The ray OS, incident at the point S on the convex surface, travels along ST after refraction.
As n2>n1, the refracted ray bends towards the Normal CSN.
Another ray OP incident, normally on the convex surface, is undeviated.
The two refracted rays do not intersect in reality but appear to meet at point I.
Thus, I is the image of the object placed at O.
OSN=i,∠CST= NSI =r
PO=-u,PI=-v ,PC=+R.
Let SCP=,∠SIP= and SOP=.
Applying Snell’s law at the point of refraction, n1sini=n2sinr.
For paraxial rays, i and r will be small. Hence, sini=i and sinr=r. Making this substitution in Equation n1sini=n2sinr.
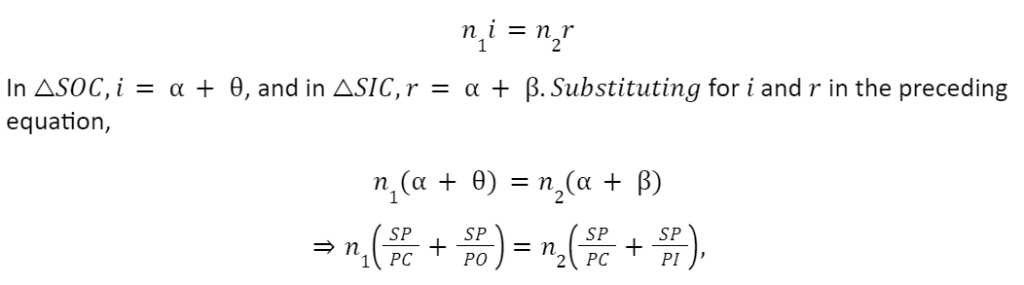

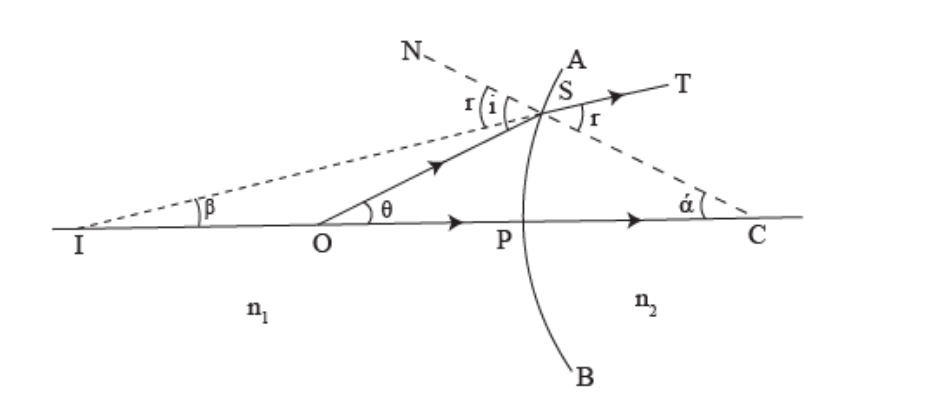
When the image is real: Consider a convex surface AB separating two media of refractive indices n1 and n2 (n2>n1), as shown in Figure.
Let P be the pole and C be the centre of curvature of the convex surface. Let a point object be placed at point O on the principal axis of the convex surface. The ray OS, incident at S, goes along SI after refraction at S. As n2>n1, the refracted ray bends towards the normal CSN. Another ray OP, undeviated. The two refracted rays intersect at I in Medium 2 . Thus, I is the real image of the object placed at O.
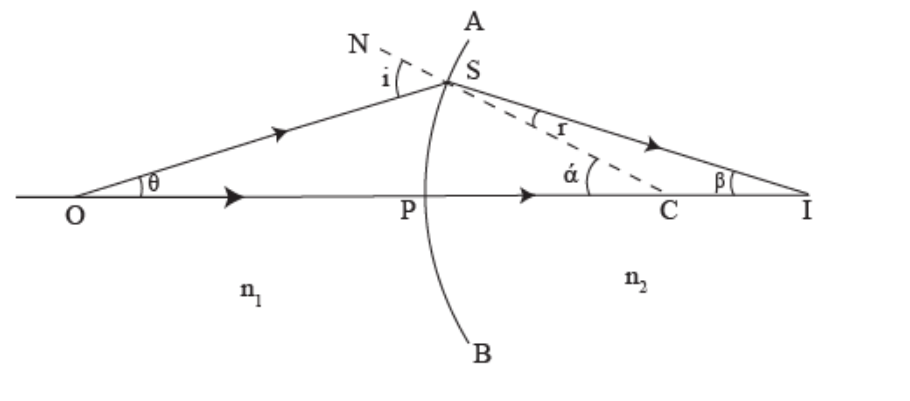

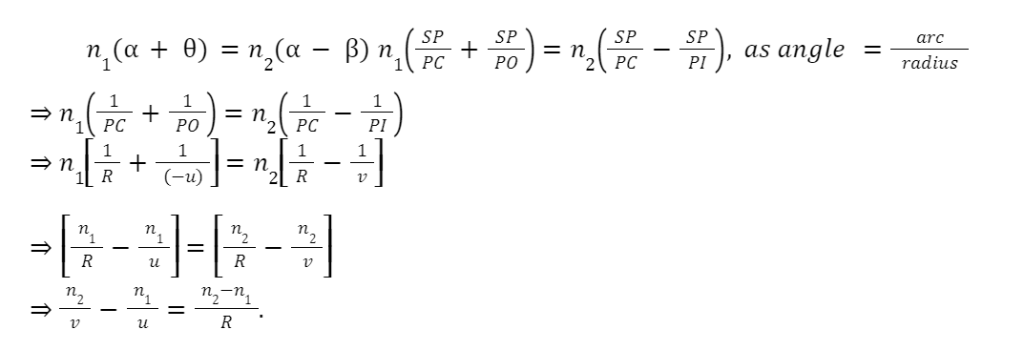
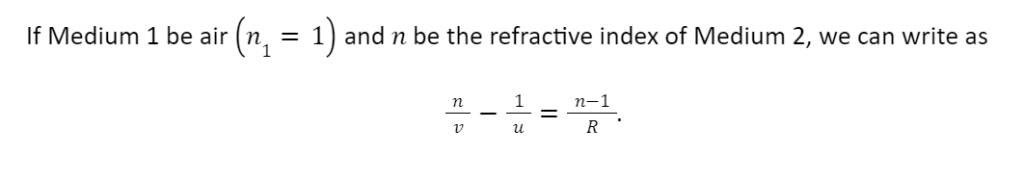
Lateral magnification:
Consider an extended object AO placed in Medium 1 (refractive index n1 ) facing a convex spherical surface MPN of Medium 2 (refractive index n2 ). Rays originating from A and O directed towards centre C will travel undeviated into Medium 2. Let the image formed be BI, as shown in Figure.
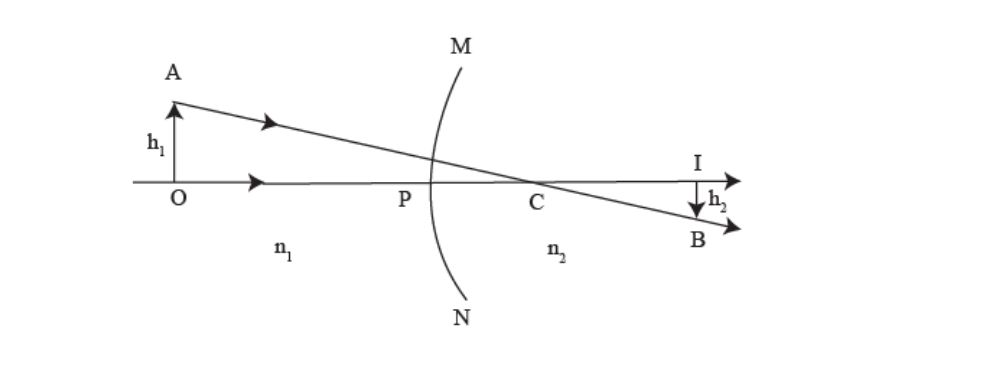
Its position may be located by using Equation

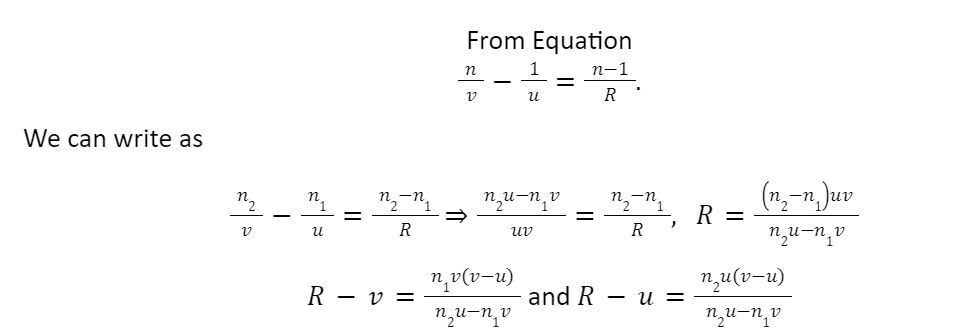
Thus,
Hence,
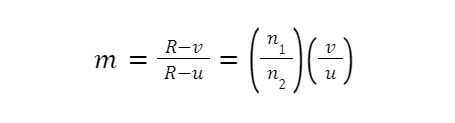
Conclusion
With this, we come to the end of the topic of Refraction at Spherical Surfaces and by Lens. Refraction is the bending of light (it also happens with sound, water and other waves) because it passes from one item into another. We hope the topic is clear to everyone.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






