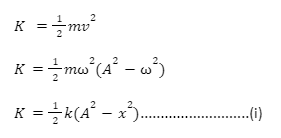Clarity On Energy In SHM

Let’s consider a pendulum in motion. The pendulum is at rest when it is in its mean position. As it moves towards its extreme position, its velocity decreases. In order to calculate the SHM energy, we must determine the particle’s kinetic and potential energy. When a particle executes SHM motion, the particle is basically doing work that is associated in the form of energy. The energy of the particle in SHM involves the Kinetic Energy of the particle and the Potential Energy of the particle with which the particle continues its motion. 

The energy of a Particle in Simple Harmonic Motion 

A particle is said to be in SHM if the acceleration acting on the particle is directly proportional to the displacement of the particle and directed towards the equilibrium position. If the particle fulfils the condition, then it is said to be in SHM. Only the energy is calculated for such a system.While discussing the energy of the particle, we talk about the two forms of energy mentioned below: 

1. KINETIC ENERGY OF A PARTICLE (K) 

Usually, the kinetic energy of the particle can be calculated in terms of displacement and also in terms of time. Let’s learn about them in detail; stepwise derivation will help you understand better.

• Deriving the expression of Kinetic Energy (KE) in terms of DISPLACEMENT 

(i) Represents the final expression for KE in terms of displacement. Here, m = mass of the particle, A = amplitude and = angular frequency. 

• Deriving the expression of Kinetic Energy (KE) in terms of TIME   

The above equation is to be used when we need to find the kinetic energy in terms of time, given the phase angle to be zero. 

2. POTENTIAL ENERGY OF A PARTICLE (U)  

The Potential Energy for a particle in SHM is represented by U. We can also calculate the potential energy in terms of displacement and time. The derivations are given below:

• Deriving the expression of Potential Energy (PE) in terms of DISPLACEMENT

The PE is given by the formula; 

U=1/2kx2+U0  

Where the potential energy at equilibrium position = U0 

When U0 = 0 then,  

U=1/2kx2

• Deriving the expression of Potential Energy (PE) in terms of TIME The expression is given as; 

U=1/2kA22(t+)

If the initial phase is zero, then 

U =1/2kA22t

U =1/2m22t   

The above formulas depict the kinetic energy and potential energy for a particle in SHM.

THE TOTAL ENERGY OF A PARTICLE (E) 

• Total energy of a particle is represented by E.
• The total energy can be calculated by adding together the expression for kinetic energy and potential energy. 
• It is known as the total MECHANICAL ENERGY of a particle. 
• The expression for total energy is: 

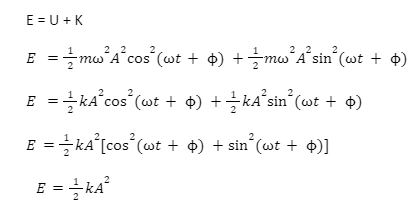
From the above expression, we can conclude that the total mechanical energy of a particle in SHM is independent of time. 

Conclusion:

This article explains energy in SHM. A particle is said to be in SHM if the acceleration acting on the particle is directly proportional to the displacement of the particle and directed towards the equilibrium position. The kinetic energy of the particle can be calculated in terms of displacement and also in terms of time. The Potential Energy for a particle in SHM is calculated in terms of displacement and time. At maximum displacement from equilibrium, potential energy is a maximum while kinetic energy is zero. An equilibrium point results in zero potential energy and a maximum amount of kinetic energy. KE is maximum at the mean position, whereas the PE is maximum at the extreme position for a particle in SHM. The total mechanical energy of a particle in SHM is independent of time.