Centripetal Acceleration

In real life, there are many objects that are constantly moving in a circular motion; our planet, for example, circles around the sun in a circular motion. It is well understood that velocity is a vector quantity, and that any object moving in a circular motion is changing velocity. Because there is a change in velocity, a force must act on the body to cause it to alter its velocity and conduct the circular motion. To fully comprehend circular motion, it is necessary to have a thorough understanding of these forces. Let’s take a closer look at centripetal force and centripetal acceleration.

Centripetal force

A centripetal force is a force that causes a body to follow a curved path (from Latin centrum, “centre,” and petere, “to pursue”). It always goes in the opposite direction of the body, toward the immediate centre of curvature of the path. “A force by which bodies are dragged, propelled, or gravitate in any manner towards a point as to a centre,” wrote Isaac Newton. In Newtonian mechanics, gravity provides the centripetal force that produces astronomical orbits.

Centripetal force is defined as a force that causes a body to travel at a constant speed along a circular route.The circumstance in which a body moves at a constant speed along a circular path is a common example of centripetal force. The centripetal force is exerted at right angles to the velocity as well as along the radius of the circular route towards the centre. Christiaan Huygens, a Dutch physicist, devised the mathematical description in 1659.

Centripetal acceleration

The rate of change of velocity is known as acceleration. Because acceleration and velocity are both vector quantities, they are direction dependent. As a result, either adjust the amplitude and direction of the velocity. Because the velocity of the object is always changing in a circular motion, there is always an acceleration. This acceleration is felt anytime a person turns a car; there is a force acting on the person as well as the steering wheel. The force is proportional to the radius of the turn and the object’s velocity. This indicates that the more power applied to the body, the sharper the turn.

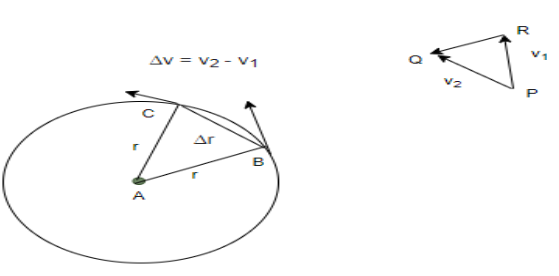
The illustration above depicts an object moving in a circular manner. Assume that the object’s speed is constant. The direction of the instantaneous velocity, as well as points B and C, are depicted in the diagram. As acceleration is defined as a change in velocity, the change in velocity is roughly directed towards the curvature’s centre.

Since the velocity is always changing and acceleration is present, acceleration points towards the centre of the curvature. Centripetal acceleration, or ac , is the name given to this type of acceleration.

“Center seeking” or “toward the centre” is what centripetal implies in this context. 

Derivation of Centripetal Acceleration

Notice how the triangles ABC and QPR are isosceles triangles in the diagram above. v1 and v2 are the names of the two sides of the vector velocity triangles. Using attributes of comparable triangles to compare the two triangles,

This gives us the acceleration of an item moving in a circular motion with a radius of “r” and a speed of “v.” This equation is inversely proportional to the radius “r” and is dependent on the square of the velocity.

Conclusion

The acceleration of a body travelling in a circular route is known as centripetal acceleration. Because velocity is a vector quantity (it has both a magnitude and a direction), while a body moves in a circular path, its direction changes all the time, causing its velocity to change, resulting in acceleration.

Centripetal acceleration is the rate at which tangential velocity changes. The net force that generates an object’s centripetal acceleration in a circular motion is called centripetal force. The centripetal force is directed towards the centre of the body, which is perpendicular to the motion of the body. The centripetal force keeps a body moving at the same speed throughout a curved path. In 1659, Christian Huygens proposed the first mathematical explanation for centripetal acceleration.