The ratio of the number of favorable outcomes to the total number of outcomes of an event is known as probability. The number of favorable outcomes can be denoted by x in an experiment with ‘n’ number of outcomes. The formula is-
Probability (Event) = Favorable Outcomes/Total Outcomes = x/n
To better understand probability, let’s look at a simple example. Assume we have to forecast whether rain will fall or not. “Yes” or “No” is the answer to this question. There is a chance that it will rain or not rain. We can use probability in this situation. Probability is used to predict the outcomes of coin tosses, dice rolls, and card draws from a deck of playing cards.
Probability
The proportion of the total number of possible outcomes to the number of outcomes in an exhaustive set of equally likely outcomes that produce a given event.
Probability Types
There are 3 major types of probabilities:
- Theoretical Probability – The chances of something happening are the basis of theoretical probability. It can also be said that it is based on the likelihood of certain events occurring in a given problem, or on previous events or a real-life situation. The probability is primarily based on open probability reasoning.
- Experimental Probability – Its name implies that it is an experiment. This implies that it will include some probability experiments. In a nutshell, the experimental probability is based on an observation made during an experiment.
- Axiomatic Probability – In axiomatic probability, there are a set of rules, or axioms that must be followed. For a set of rules known as Kolmogorov’s three axioms, these rules are applied to all types of reasons. We can calculate the chances of occurrence and non-occurrence of any event using axiomatic probability.
Probability Theory Terminology
The terms in probability listed below will aid in a better understanding of probability concepts.
Experiment: An experiment is a trial or operation that is carried out to produce a specific result.
Sample space: A sample space is made up of all the possible outcomes of an experiment put together. Tossing a coin, for example, has a sample space of head and tail.
Favorable Outcome: A favorable outcome is an event that has produced the desired result or expected event. For example, if we roll two dice and get the sum of the numbers on the two dice as 4, the possible/favorable outcomes are (1, 3), (2,2), & (3,2). (3,1).
Trial: A trial is a term that refers to a random experiment.
Exhaustive Events: An exhaustive event occurs when the set of all possible outcomes of an experiment equals the sample space.
Probability formula
The probability formula determines the likelihood of an event occurring. It’s the proportion of positive outcomes to total positive outcomes. The probability formula is as follows:
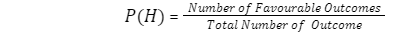
Probability formula with addition rule:
P(A or B) = P(A) + P(B) – P(A∩B)
P(A B) = P(A) + P(B) – P(AB)
Probability formula with the complementary rule:
P(A’) = 1 – P(A).
P(A) + P(A’) = 1.
Formula for probability with the conditional rule: When the probability of event B is desired and event A is already known to have occurred,
P(B, given A) = P(A and B), P(A, given B).P(B∣A) = P(A∩B)/P(A)
Probability formula the multiplication: When an event is the intersection of two other events, that is, when events A and B must occur simultaneously, then
P(A and B) = P(A)P(B).P(A∩B) = P(A)P(B∣A)
Probability Example
Using the probability formula, calculate the chances of getting a number less than 5 when rolling a dice.
Solution: The chances of getting a number less than 5 are slim.
Given: 1,2,3,4,5,6 sample space
1,2,3,4 = Getting a number less than 5
As a result, n(S) = 6 and n(A) = 4.
P(A) = (n(A))/(n(s)) p(A) = 4/6 m = 2/3 Using the Probability Formula
Probability distributions
A probability distribution is a statistical function that describes all of the possible values and probabilities for a random variable within a given range.
- Convert all of the percentages to probabilities in decimal form
- Draw a table of probability distributions
- Multiply each column’s values
- Combine the results from steps 3 and 4
Probability Distributions Types
Probability distributions are classified in a variety of ways.
- chi- square distribution
- binomial distribution
- Poisson distribution
Probability Distributions Use
In statistics is the probability distribution. It has a wide range of applications in fields such as business, engineering, medicine, and other major industries. It’s mostly used in random experiments to make future predictions based on a sample. For example, in business, it is used to predict whether a new strategy will result in profit or loss for the company, or in the medical field, it is used to prove any hypothesis test.
Conclusion
The ratio of the number of favorable outcomes to the total number of outcomes of an event is known as probability. The number of favorable outcomes can be denoted by x in an experiment with ‘n’ number of outcomes. Probability theory is mostly useful in making predictions. Estimates and predictions are crucial components of any research project. As a result, statistical methods are heavily reliant on probability theory.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






