THE RANGE OF A FUNCTION

Functions in math are just like a vending machine. We give money as input (domain) to the vending machine and get some chocolates or cookies in return as the output. The chocolates or cookies that the vending machine returns us is its range. 

Thus, the meaning of range is the set of all the possible outputs that we get on substituting the domain in the function. 

HOW TO FIND THE RANGE OF A FUNCTION?

Method 1 :

Since, range is the set of all possible values of the output of a function, we can easily calculate it if we know the minimum and maximum value of a function. It is obvious that all the possible values of a function will lie within the minimum and maximum values of the function. Therefore, the range of a function can be calculated by calculating its minimum and maximum value.

Let’s calculate the range of the function f(x)=x-1

We know that the square root function never gives a negative value. Therefore, its minimum value will be 0.

As we keep on increasing the value of x, the value of f(x) goes to infinity. Therefore, the maximum value of f(x) will be infinity.

Now, we know that all the possible values of f(x) lie between its minimum and maximum value. Thus, the range of f(x) will be [0,∞)

Method 2 :

 We can find the range of a function using a graph. It is the most effective way to find the range of any function. 

To find range using a graph, follow the below steps :

1. Draw the graph of the given function
2. Note down the minimum and maximum value of the variable y on the y-axis over which the graph is spread
3. The range of the function will be [minimum y value, maximum y value]

Let’s find out the range of the function f(x)=sin x

We know that the graph of sin x is represented as below :

f(x)=sin x

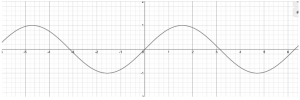
We can see from the graph that the minimum value of y is -1 and the maximum value of y is 1

Therefore, the range of the function f(x)=sin x is [-1,1]

EXAMPLES

• Find the range of the function f(x)=x2+5

We know that x2 is never negative.

Therefore, x2≥0 for all real values of x

            ⟹x2+5 ≥ 0+5

                                   ⟹x2+5 ≥ 5

                        Thus, the minimum value of f(x) is 5

            As we keep on increasing the value of x, the maximum value of f(x) goes to infinity.

Hence, the range of the function f(x) is [5,∞)

• Find the range of the function f(x) = 1x-9

If we keep on either decreasing or increasing the value of x, we find that the value of f(x) tends to become 0, but it never becomes 0. That means that f(x) is taking all the values except x=0.

Thus, the range of f(x) will be “all real numbers except 0”.

We can also solve this question using the graph method. The graph of f(x) is represented as below :

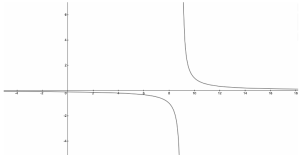
We can see from the above graph that the function f(x) takes all the values on the y-axis except 0. Thus, the range of f(x) is “all real numbers except 0”.

• Find the range of f(x)=x2 +4

We know x2 can never take negative values. Therefore,

⟹x20

⟹x2+4≥0+4

⟹x2+4≥4

⟹x2 +44

⟹x2 +4≥2

Thus, a minimum value of f(x) is 2

As we keep on increasing the value of x, the maximum value of f(x) goes to infinity.

Hence, the range of the function f(x) is [2,∞)

Conclusion

The range is an important parameter that defines a function. One must know how to find the range of a function to know how the function behaves and what are its limits. We have discussed two methods to find the range of a function. It is always easier and more effective to find the range of a function using the graphical method. But one must have the knowledge of graphs of the functions one is dealing with.