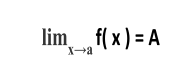Profile
Settings
Refer your friends
Sign out
The value that the function approaches as its argument approaches aa is the limit of a function at a point aa in its domain (if it exists). The concept of a limit is at the heart of calculus and analysis. It is used to define the derivative and the definite integral, as well as to examine the local behavior of functions near points of interest.
Informally, a function is said to have a limit LL at aa if it is possible to randomly close the function to LL by selecting values closer and closer to aa. It should be noted that the actual value at aa has no bearing on the value of the limit.
Limits
A limit is defined in mathematics as the value at which a function approaches the output for the given input values. Limits are used to define integrals, derivatives, and continuity in calculus and mathematical analysis.
Limits of a Function
The value that a function (or sequence) approaches as the input (or index) approaches some value is referred to as a limit. Limits are used to define continuity, derivatives, and integrals in calculus and mathematical analysis. Two different limits can be approached by a function. One in which the variable approaches its limit by using values greater than the limit, and the other in which the variable approaches its limit by using values less than the limit. The limit is not defined in this case, but the right and left-hand limits exist.
Formula of Limits
As a function of x, let y = f(x). If f(x) takes indeterminate form at a point x = a, then we can consider the values of the function that are very close to a. If these values tend to some definite unique number in the same way that x tends to a, then the obtained unique number is referred to as the limit of f(x) at x = a.
The formula can be written as follows:
where, f(x) is a mathematical function.
x is a variable that is getting close to the value a.
It is interpreted as the limit of a function of x equals A as x approaches a.
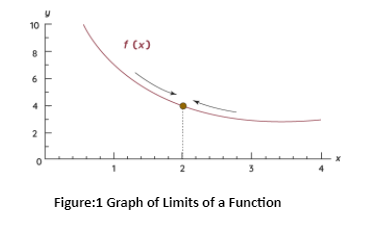
Graph of Limits of a Function
A graph is a visual way of determining a function’s limit. If the function has a limit as x approaches a, the graph’s branches from the left and right will approach the same y− coordinate near x=a.
In mathematics, limits are distinct real numbers. Consider a real-valued function “f” and a real number “c,” and the limit is normally defined as limx → c f( x ) = L
It is interpreted as “the limit of f of x as x approaches c equals L. The “lim” represents the limit, and the right arrow represents the fact that function f(x) approaches the limit L as x approaches c.
Finding Limits of a Function
Determine the limit by locating the lowest common denominator.
- Locate the LCD of fractions on the top.
- Distribute the denominators on top.
- Add or subtract the numerators before cancelling terms.
- To make things even easier, apply the fraction rules.
- Simplify by substituting the limit value into this function.
Limits’ Properties
Here are some properties of the function’s limits: If the limits limx→a f(x) and limx→a g(x)exist and n is an integer, then
The Law of Addition
limx→a [f(x) + g(x)]=limx→a f(x) + limx→a g(x)
Subtraction Law:
limx→a [f(x) − g(x)] = limx→a f(x) − limx→a g(x)
Multiplication Law
limx→a [f(x)⋅ g(x)] = limx→a f(x)⋅limx→a g(x)
Divisional Law
limx→a [f(x) /g(x)]=limx→a f(x)/limx→a g(x), where limx→a g(x)≠0
The Power Law limx→A C=C
Conclusion
The value that the function approaches as its argument approaches a.a is the limit of a function at a point aa in its domain (if it exists). The concept of a limit is at the heart of calculus and analysis. It is used to define the derivative and the definite integral, as well as to examine the local behavior of functions near points of interest. Limits are used to define integrals, derivatives, and continuity in calculus and mathematical analysis. It is used during the analysis process and always refers to the behavior of the function at a specific point.
