An event is a subset of a sample space. In other terms, an event is a collection of the results of a random experiment. Capital letters are used to indicate it.
An event can be getting any of the numbers from 1 to 6 on the uppermost face of a die in a random experiment. Any of the conceivable events’ probability can be calculated. The possibility of getting 5 in a single die throw is 1/6.
Simple Event
Any event is Simple if it corresponds to only one conceivable experiment outcome. In other terms, a simple event is one that has only one sample point in a sample space. The sample space in a random die-throwing experiment is
S = {1, 2, 3, 4, 5, 6}. The event of getting 5 on the highest face, E, is a simple event.
Compound Event
If an event relates to more than one conceivable experiment outcome, it is called compound. In other terms, a compound event is one that has more than one sample point in a sample space. The sample space in a random die-throwing experiment is
S = {1, 2, 3, 4, 5, 6}. The event E of getting the multiple of 2 is considered a compound event which is given as E = {2, 4, 6}.
We can conduct some algebra on events using Set theory. The union or intersection of events is one of them.
Complimentary Event
Complementary to any occurrence, as the term implies, reveals its opposing side. The complimentary event E’ displays not E for any event E. Every result that isn’t in E is considered to be in E’. Simply put, if E indicates that the glass is half empty, E’ indicates that the glass is half full.
Let us consider an example of throwing a die. The data in sample space is given as, S = {1, 2, 3, 4, 5, 6}. E shows the event of getting an even number i.e., E = {2, 4, 6}. The event E’ shows the outcome of not an even number or getting an odd number. E’ = {1, 3, 5}.
Exhaustive Events
A random experiment’s whole number of possible outcomes is an exhaustive event. When you combine the events of receiving an odd number and getting an even number in a single die toss, you have an exhaustive event.
Favourable Events
In a random experiment, the number of results that demonstrate the event occurring are desirable events. They display the amount of circumstances in which an event is beneficial. The number of favourable events for receiving two tails together in a random experiment of tossing two coins is 1.
Mutually Exclusive Events
Events are mutually exclusive if the occurrence of one of them eliminates the possibility of the occurrence of the other in the same trail. We can also claim that no two or more of the occurrences can occur at the same time. When throwing a coin, the occurrences of head and tail are mutually exclusive. Only one of them is possible.
Equally Likely Events
A situation in which all possible outcomes have an equal chance of occurring. When rolling a dice, all six faces have an equal chance of appearing.
Independent Events
Two occurrences are independent if they have no effect on each other’s happening or non-happening. When tossing a die, getting 2 on the first throw has no bearing on the outcome of subsequent throws.
Chance Events
We are surrounded by randomness. Probability theory is a mathematical framework that allows us to logically understand chance events. The probability of occurrence is a number which shows how probable it is to happen. This number is always in the range of 0 to 1, with 0 denoting impossibility and 1 denoting certainty.
A fair coin toss, with two probable outcomes of heads or tails, is a classic example of a probabilistic experiment. The likelihood of flipping a head or a tail is 1/2 in this situation. We may acquire more or fewer than 50 percent heads in a real sequence of coin tosses. However, as the number of flips rises, the long-run frequency of heads will inevitably approach 50%.
The two outcomes of an unfairly or weighted coin are not equally likely. Drag the true probability bars (on the right in blue) up or down to adjust the coin’s weight or distribution. We can build the statistical object known as a random variable by assigning numbers to the outcomes, such as 1 for heads and 0 for tails.
Expectation
A random variable’s expectation is a number that seeks to capture the random variable’s distribution’s centre. It can be thought of as the long-run average of a large number of independent samples drawn from a specific distribution. It is specified as the probability-weighted sum of all potential values in the support of the random variable.
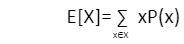
Variance
The variance of a random variable measures the spread of that random variable’s distribution, whereas expectation offers a measure of centrality. The mean result of the squared difference between the random variable and its expectation is the variance.
Var(X)=E[(X−E[X])2]
Conclusion
Probability is a number between 0 and 1 that represents the probability of an event occurring. A probability of 0 indicates that there is no chance that the event will occur, whereas a probability of 1 suggests that the event will occur. The addition rule, the multiplication rule, and the complement rule are the three main rules related with basic probability.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






