It is easy to see that complex numbers and vectors have a lot in common when plotting them on an Argand diagram. For example, adding and subtracting complex numbers is the same as adding and subtracting vectors in terms of geometry. There are two characteristics of a vector: its direction and magnitude. A complex number must also have these two characteristics. It is important to remember that the size of a complex number is called its modulus. To figure out the direction of a complex number, look at its argument.
Complex numbers
Apart from real numbers, there exist a set of numbers of the from a+ib.This type of number is called a complex number. It is used to represent the square root of negative numbers. Scientific research, fluid dynamics, quantum mechanics, and signal processing are examples of where complex numbers can be beneficial.
A complex number can be thought of as the sum of an imaginary number and an actual number, like this: a+ib can be written as a+z. Each number in this sentence is an exact number, like ‘a’ and ‘b’; a is said to be the fundamental part, and b is said to be the imaginary part, which is called Im (z). It is also a number that is not real. In this case, complex numbers are 2 + 3i and -2 -5i, examples. (i) is called iota, and it is used to show the imaginary part of complex numbers, which is written with an (i) in it.
Definition: Argument of a complex number
It is the angle, in radians, between the positive real axis and the line between the origin and the complex number, measured counterclockwise. The argument is called Arg (z), which is short for ‘arg’.
It’s common for the argument of a complex number to be given in this range: (-Π,Π)
However, we can also talk about a complex number with a view that it is greater than or less than. This is the principal argument for a complex number in the range [-π, π]. Some people use the content from zero to two for the main idea. This isn’t very common, though.
In right triangle trigonometry, we can figure out the complex number’s argument when given the Cartesian form of the number a + ib.
The angle is given by tan-1(b/a) and the principal argument lie between (-Π,Π) only.
Finding the argument of a complex number in radians
A complex number has an ‘argument’: the angle between the positive real axis and the line that connects its origin to its complex number in radians. The argument of a complex number, by convention, is given in the range between [-π, π].
In the first step, we write down the complex number on an Argand diagram.
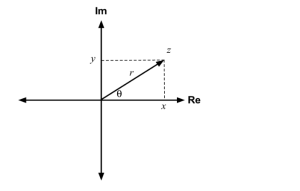
We have called the complex number’s argument in the Argand diagram above. This is how it should be written. We can see that this complex number has an angle in the right triangle whose sides are blue, green, and purple lines. This angle is the argument of this number.
This angle can be found by using the trigonometric properties of a right-angle triangle.
Properties of the argument of a complex number
Let’s talk about a few things that all the arguments of complex numbers share. When you think about it this way, let’s say that z is a complex number and n is some number. Then, let’s say that z is a nonzero complex number and
arg(nz) = n arg(z)
When we think about complex numbers z1 and z2, these are the following:
- arg (z1/ z2)= arg ( z1) – arg ( z2)
- arg ( z1 /* z2) = arg ( z1) + arg ( z2)
Principal vs general argument of a complex number
The angle made by the line representation of the complex number with the positive x-axis is called the argument of the complex number. This angle is called the complex number’s angle. These values make this angle have a ‘principal value’, which means it has a ‘general value’, which means it has a ‘principal argument’ and a ‘general argument’. Trigonometric value Tan is used to find the complex number’s argument, which is based on the general answer to the trigonometric tangent function, so it is called Tan.
Applications of the argument of a complex number
The argument of a complex number can be used to change the complex number into a polar form, and it can also be used to figure out how the real and imaginary parts of the complex number are linked. Using the angle, you can tell if the fundamental factor is more significant or the imaginary part is more considerable. The argument value of a complex number is the angle. When the real and imaginary parts are equal, the fundamental factor is more significant than the imaginary part. When the real and imaginary parts are similar, the essential element is more important than the imaginary part. When the real and imaginary parts are equal, the fundamental factor is more significant.
Conclusion
Every polynomial with complex coefficients has roots in complex numbers because complex numbers were added to maths. This introduction also helped to open the door to creating a new kind of number, which could be used to solve and explain many different types of problems.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






