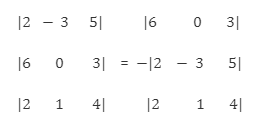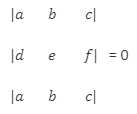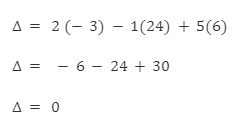Switching Property and Repetition Property

Properties of Determinants: Switching Property and Repetition Property

The determinant is a special way of representing algebraic functions and terms. We denote determinant as P, det P or  | P|. We calculate determinants from the square matrix. The  square matrix is the one that has the same number of rows and columns. 

a    b

c     d

This matrix has two columns and two rows; therefore, it is a square matrix of 2×2. 

| a  b  c |

| d  e  f |

| g  h  i |

This matrix has three rows and three columns. The square matrix is of order 3×3. 

We expand a matrix to find its  determinant as: 

a (e × i – h × f) – b (d × i – g × f) + c (d × h – g × e)

In this article, we will be learning about the properties of determinants, including Switching Property and Proportionality (Repetition) Property. 

Properties of Determinants

There are various properties of determinants. Some of them are as follows:

• Reflection Property: The determinant of a matrix stays unaltered if we exchange rows with the columns. 
• Zero Property: If all the elements of a row or column are zero, then the determinant of the matrix is zero.
• Proportionality (Repetition) Property: If any two rows or columns of a matrix are the same, then the determinant becomes zero. 
• Switching Property: Upon changing any two rows or columns of a matrix, its determinant sign changes. 

• Scalar Multiple Property: If all the elements of a determinant’s row (or column) are multiplied by a non-zero constant, then the determinant gets multiplied by the same constant.

There are other properties of determinants, such as sum property, property of invariance, factor property, and determinant of cofactor. In this article, we will focus on two properties of determinants: switching property and repetition property. Let us learn about them one by one. 

Switching Property of Determinants

According to the ‘Switching Property of Determinants’, if we switch elements of any two rows or columns, the sign of the determinant gets changed. We have determinant given as: 

| a  b  c |

| d  e  f |

| g  h  i |

If we switch any two rows, say R1 and R2:

| b  a  c |

| e  d  f |

| h  g  i |

Then we get: 

| a  b  c |         | b  a  c |

| d  e  f |  =  – | e  d  f |

| g  h  i |         | h  g  i |

For example:

If we interchange R1 and R2, the sign of determinant will change as:

The determinant is multiplied by (-1) on switching the rows or columns. 

Repetition Property of Determinants

As per the repetition property of the determinant, if any two rows or columns of the matrix are equal, the determinant becomes 0. 

Let us take an example to prove the property. 

Therefore, if all the determinant elements are equal, then the determinant of the matrix is equal to 0. 

Conclusion

In this study material, we learned about two of the most important properties of determinants, the repetition and switching property. We use these properties to calculate the matrix of the equation. The determinant is only for the square matrix or order type 2×2, 3×3, and so on. 

In this article, we also learn about some other properties of determinants, such as zero property, scalar multiple property, and so on. Finally, using some examples, we saw how to use the properties of determinants to calculate them.