Representation of Relation Between Two Sets

In the language of mathematics, how do you express the students of a class, the employees in a company, or simply a group of randomly chosen colours? The answer is simple—sets. A set is a collection of distinct objects forming a group, which can have natural numbers, whole numbers, real numbers, or even days of a week, types of vehicles, etc. Eg. A= {1,2,3,4,5}

Now, a set’s elements can be uniquely related to each other or the elements of a different set. For example, In a class, students can be friends among themselves or with the students of another class. In mathematics, such mappings are called relations.

Let’s understand further what relations are and how they are represented. And also types of sets in mathematics.

Relations in Mathematics

Cartesian Product

Before we understand this, let’s understand the concept of Cartesian products.

Let’s say we have two sets: A= {1,2} and B= {1,7,8}. We know that you can multiply two vectors (scalar and vector products) or two matrices. Descartes claimed that it was possible to multiply two sets in the same way—map each element of the first set with each element of the second.

Thus A × B= {(1,1), (1,7), (1,8), (2,1), (2,7), (2,8)}. This product is called the Cartesian product of sets. Each element, e.g. (1,1), is called an ordered pair. 

Note:

• The order of the elements is important in an ordered pair. (1,7) ≠ (7,1). Consequently, 

A × B ≠ B×A

• It follows from the definition that n (A × B) = n(A)n(B)
• Cartesian products are essentially set and follow all the properties.

Relations

A relation in Mathematics is a subset of the Cartesian product of two sets. The elements of the ordered pair in a relation follow a set rule.

Let’s take the sets A= {1,2,3} and B= {4,7,8,9}. We define a relation R: A→B.

R= {(a, b): a ∈ A, b ∈ B, b=a²}, where b is the image of preimage a.

By this rule, 2 from A can be mapped with four from B. Therefore (2,4) becomes a member of R. Similarly, three can also be mapped with 9. None of the other elements of A can be mapped this way.

Therefore, R = {(2,4), (3,9)}.

NOTE

• A relation is defined between two sets and is directional. For instance, R in the above example is defined from A to B.

• It is generally denoted by R.

• For any relation, the domain is the set of all its preimages. For R, domain D_R = {2,3}.

• For any relation, the range is defined as the set of all its images. For R again, range R_R = {4,9}.

• For any relation, the co-domain is the set from which the images derive their values. For R, the co-domain is set B.

• Implicitly, the range is always a subset of the co-domain.

Representation of Relations

Let’s say we have two sets, A and B. A = {1,2,3} and B = {0,1,2,4}. We want to represent a relation R which contains all the ordered pairs (a, b), where a ∈ A, b ∈ B, and a ≤ b.

There are many ways to represent the relation R. Down below, we have discussed the six most common ones.

Roaster form, or listing method

This method simply lists the ordered pairs of the relation R in a set. 

R_A→B = {(1,1), (1,2), (1,4), (2,2), (2,4), (3,4)}

Set Builder form

In this method, you state the conditions that the ordered pairs of the relation must satisfy. Using these conditions, it must be possible to derive R in its roaster form.

R_A→B = {(a, b): a ∈ A, b ∈ B, a ≤ b}

Statement Representation

As the name suggests, you write down the relation in statements, stating every condition that the relation abides by.

E.g., For all a∈ A, b ∈ B, a is related to b if and only if a ≤ b.

Matrix Representation

A matrix can represent the ordered pairs of the Cartesian product of two matrices A and B, wherein the elements of A can denote the rows, and B can denote the columns. For every ordered pair thus obtained, if you put 1 if it exists in the relation and 0 if it doesn’t, you get the matrix representation of the relation.

For A = {1,2,3} and B = {0,1,2,4}, and R_A→B = {(a, b): a ∈ A, b ∈ B, a ≤ b}, we’ll have a 3×4 matrix as follows.

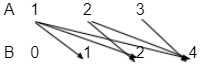
Graph Representation

You write all the elements of a set in a row. This way, you obtain two rows—domain and co-domain. Use arrows to map the preimages with their images to represent the relation.

For A = {1,2,3} and B = {0,1,2,4}, and R_A→B = {(a, b): a ∈ A, b ∈ B, a ≤ b},

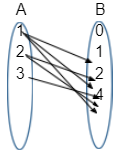
Arrow Diagram Representation

It is a simple diagrammatic representation of the relation R.

For A = {1,2,3} and B = {0,1,2,4}, and R_A→B = {(a, b): a ∈ A, b ∈ B, a ≤ b},

Types of Sets

The following are the major types of sets:

1. Finite Set: This kind of set has a fixed number of elements. Eg. Factors of 8.
2. Infinite Set: These sets have an infinite number of elements. Eg. Multiples of 8.
3.  Empty Set: This set has no elements. It’s generally denoted by the symbol ∅.
4. Singleton Set: This set has only one element.