There are a lot of numbers that are only pure imaginary but not accurate. There are a lot of pure imaginary numbers, and this lesson will show you how to evaluate them, simplify or divide them, multiply them, and solve equations.
Learning how to work with imaginary numbers will help us work better with complex numbers.
In the past, complex numbers were linked to the idea of solving equations. In the 16th century, mathematicians tried to find algebraic solutions to the cubic equation. When they tried to solve equations, they found that many had real-world solutions. However, the methods used to solve them led to the need to find the square roots of negative numbers. The way of solving cubics that Tartaglia used often made it necessary to figure out the square root of negative numbers even when the solutions were all real, even though they were all real.
Definition: Imaginary numbers
There are two types of complex numbers: one that is real and one that is not real. An imaginary number has the form bi, where the first number is real and the second is imaginary.
People need to know that imaginary numbers are part of another set called complex numbers, and they are not the same as real ones. Let’s also remember what complex numbers are.
Imaginary numbers chart
There is also an interesting thing about it. The value changes four times when you multiply it. Because √-1= i when you multiply it by itself, for example, In that case, i⨯i = -1. In this example, -iis the answer. That makes it all the way around. This makes it easy to figure out how many exponents of I you need to work out. If:
i = √-1 i2 = -1 i3 = -√-1 i4 = 1 i5 = √-1 and so on.
This cycle will go on through the exponents, also called the imaginary numbers chart, and will keep going. Knowledge of how imaginary numbers grow is practical when multiplying and dividing imaginary numbers. It is possible to use the rules of exponents to apply to I after grouping the coefficients and fictional terms. The real numbers are then multiplied as usual. The same thing happens when you divide things up, too. By following the same rules for multiplying and dividing real and imaginary numbers, you can make them easier to work with, like variables and coefficients.
This isn’t the only time that imaginary numbers have been in pop culture.
Pure imaginary numbers
The number i is not alone! We can make infinitely many pure imaginary numbers by taking multiples of this imaginary unit and adding them together.
When you take the squares of these numbers, you can see how they connect to the real numbers. Let’s find out how this works by squaring the number 3i. The properties of integer exponents stay the same, so we can square 3i, just as we’d think we would be able to do.
(3i)2=(3)2⨯i2
We know that i2=-1 hence the answer is -9.
Why do we have imaginary numbers anyway?
The answer is straightforward. The imaginary unit ‘i’ can help us solve many equations that don’t have real number solutions.
Many equations can’t be solved in one number system, but another, more general one can solve them.
Here are some examples why we need different types of numbers.
- We can’t solve x+8=1; we need integers for this!
- To solve 3x-1=0, which means that 3x minus 1, equals 0, we need rational numbers. We can’t do this with only integers.
- We can’t solve x2 with only rational numbers hence we developed irrational numbers.
- The square of 2 is 2×2. It’s time to get into the irrational numbers and the actual number system.
As we saw in the above examples that only integers of rational numbers were not sufficient to define maths therefore we developed irrational numbers.
Similarly,real numbers can’t help us solve x2=-1, squared, equals, minus, 1, so we can’t do that. It will help us if we use imaginary numbers for this task!
Classifying the New Types of Numbers
Pure imaginary numbers are a group of numbers made by taking the square roots of negative numbers and then adding them together. In symbols, we could write a pure imaginary number as bi, the product of a natural number b, and an imaginary number i. They are not on the number line, so there is no place for them on the number line.
It’s also possible to talk about adding an actual number to a purely imaginary number. When you do this, you get what is called a complex number. A complex number has the form a+bi, where an is a natural number and bi is a number that is only pure imaginary.
If these numbers aren’t on the number line, can we make pictures of complex or imaginary numbers by putting them on paper? Yes, that’s true. But a one-dimensional number line won’t be enough for you. It needs to be on a second number line to show the pure imaginary part of the complex number. In other words, we need to show complex numbers with a two-dimensional picture to do that. The number 2+3i is shown as a point in this picture.
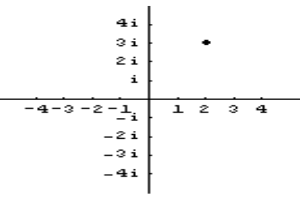
So the actual numbers are points on the horizontal axis, which is where they are. Imaginary numbers are those numbers that aren’t real and aren’t on the horizontal axis, so they are not real. It’s like this: Pure imaginary numbers are points on the vertical axis (other than the origin). Complex numbers include all the possible issues in the picture, covering the whole thing. There are a lot of different kinds of numbers that are real. Odd numbers are just like them also. Just like a whole number is also a fraction, so is a fraction.
Conclusion
An actual number multiplied by the imaginary unit I is known as an imaginary number.- b2 is the square of an imaginary number bi, a number that isn’t real, such as 5i, has a square that’s -25. As a general rule, zero is both real and imaginary, so it is both.Complex numbers are used at the places where real numbers fail to give the solution. For example, the solution of equation x 8=-1 cannot be given by real numbers.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






