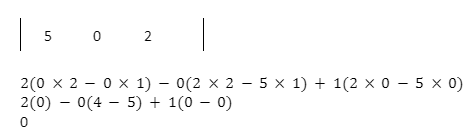Properties of Determinants

A matrix is a collection of functions and numeric values represented in a table form. The determinant of a matrix is a single numeric value. If M represents a matrix, then we can represent the determinant as | M | or det M. The properties of determinants help find the value of determinants without doing long calculations. In this article, we will learn about the two essential properties of determinants: reflection property and all-zero property.

Necessary Conditions

Before we proceed further, let us look at some of the important conditions to satisfy the properties of determinants:

• Multiplicativity; det (XY) = det (X) det (Y)

• Invariance under transpose det (X) = det (X’)

• Invariance under row operations, if we add multiple of any row or column to another row or column, then det (X) remains the same.

• Upon interchanging any two rows or columns, the sign of the determinant changes.

How are Determinants Different from Matrices?

Determinants and matrices are two different mathematical concepts. Both matrices and determinants have several practical applications. The point of difference between matrices and determinants is:

• The matrix is a set of functions or numeric values represented between square brackets in the form of a table. The determinant is a single numeric value. 

• The number of rows and columns of a matrix can be the same or different. For determinants, the number of rows and columns are always the same. 

• In matrices, we use simple mathematical operations to find the unknown variable. In determinants, other rules such as Cramer’s Rule are used.

Now, let us learn about three essential properties of determinants one by one.

Reflection Property

As per the reflection property of the determinant, if we interchange rows and columns, then the determinant remains unaffected. Let us understand this with an example:

We are given,

In both cases, the determinant is the same. Hence the reflection property is proved.

All-Zero Property

If all the terms of a row or column are zero, the determinant will be 0. This is known as an all-zero property.

Conclusion

The properties of determinants make it easier to calculate the value of determinants. In this article, we learned about all-zero and reflection properties. Using these two, we can find the determinant easily and quickly. There are various other properties that we can use to derive the correct value of the determinant. Determinants is an important topic in competitive exams and have various real-life applications also like keeping a track of similar data in form of rows and columns or finding a solution to linear equations in a systematic manner. Hope you liked the article