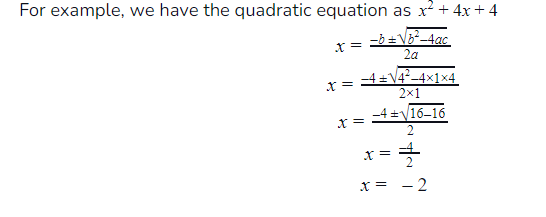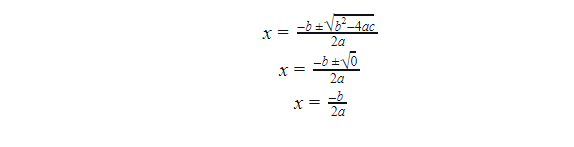Number of Solutions in a Quadratic Equation

The algebraic polynomials are the functions formed by the combination of variables and constants. The polynomial that has degree 2 is known as the quadratic equation. The degree is the highest power of the function.

The standard form of the quadratic function is given by:

ax²+bx+c

Here,

a is the coefficient if x2

b is the coefficient of x

c is the constant term.

In this study material, we will be learning how to find the number of solutions in a quadratic equation.  

How to Find Number of Solutions in a Quadratic Equation

The degree of the polynomial determines the number of solutions an equation has. The quadratic equation always has two solutions of the variables. The solutions can be negative, positive, same, or different.

To understand this, let us take an example, let us find out the solutions of the few quadratic equations.

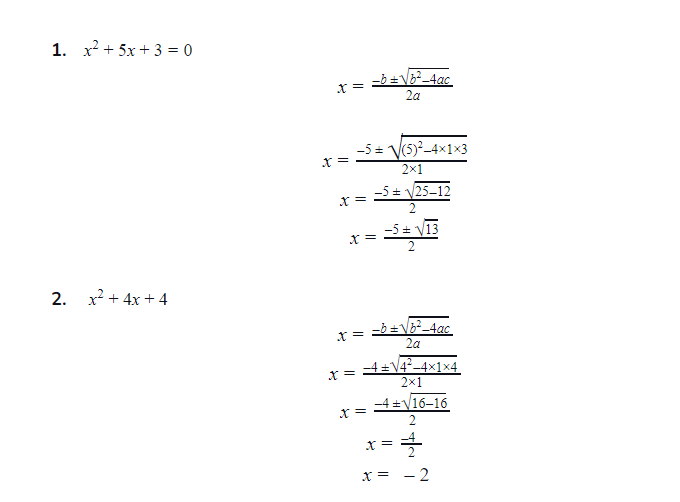
Now, this is the method through which we find out how many solutions to the quadratic equation. But there is another method to know how many solutions quadratic equations will have and about their nature too.

By calculating the discriminant of the equation, we can determine the number of quadratic equation solutions.

Now, what is discriminant?

We know the quadratic formula is given by:

Here,

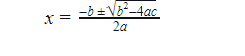
a is the coefficient if x2

b is the coefficient of x

c is the constant term.

The b2-4ac is known as a discriminant represented as D.

• If D > 0, then the solution of the quadratic equation has two real solutions, both of them being distinct.

Example: x2+5x+2

 D=b2-4ac

D=52-412

D=25-8

D = 17

Since D > 0, hence the equation has two real solutions.

• If D < 0, then the solution of the quadratic equation has two imaginary solutions, both of them being the same.

Example:  x2 + 2x +4

D=b2-4ac

D=22-414

D=4-16

D = -12

Since D < 0, hence this equation has two imaginary solutions.

• If D = 0, then the solution of the quadratic equation has two real solutions, both being equal.

Example: x2+2x+1

D=b2-4ac

D=22-411

D=4-4

D = 0

Since D = 0, hence the equation has two real solutions that are the same.

Solved Questions

1. How many real solutions does the quadratic equation 3×2-2x=-1 have?

The equation is 3×2-2x+1=0

D=b2-4ac

D=(-2)2-431

D=4-12

D = -8

Since D < 0, the equation will have no real solution.

2. Is the root of the quadratic equation of x2+x+1 real or imaginary?

x2+x+1

D=b2-4ac

D=12-411

D=1-4

D = -3

Since D < 0, the root of the equation will be imaginary.

3. Find the discriminant of the equation 2×2+5x+2=0

D=b2-4ac

D=52-422

D=25-16

D=9

4. Find the nature of the quadratic equation x2+2x+1=0

D=b2-4ac

D=22-411

D=4-4

D=0

The roots are the same and real.

Conclusion

The quadratic equation of the standard form ax2+bx+c has two solutions. The solutions or roots of quadratic equations can be positive/negative, same/distinct, and real or imaginary. To determine the nature of the quadratic equation, we find the determinant. The determinant of the equation is calculated by the formula x=-b b2-4ac 2a, where all variables have the usual meaning.

The imaginary solutions lead to complex solutions of quadratic equations. About which you will be learning in the section of complex numbers.