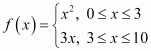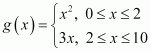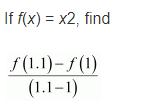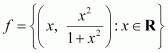Miscellaneous Problems on Relations

Introduction

A link of two sets is an accumulation of ordered sets containing one item from each set. Assuming the item x is from the primary set and the item y is from the subsequent set, then, at that point, the items are supposed to be linked if the cartesian product (x,y) is related. This is otherwise known as a binary relation. The mathematical function is an example of a relation. As relations are sets, they fulfil the laws of variable-based math of sets.

Moreover, they can be controlled by utilising set activities, including union, intersection and composition. Binary relations are vigorously utilised in software engineering, such as relational database management systems (RDBMS). This article discusses the problems on relations with examples solving miscellaneous problems on relations with detailed equations.

Examples of Problems on Relations

X and Y are sets of all real numbers. So when each element ‘x’ in set X is equal to each element ‘y’ in set Y, the expression will be:

y = x

=>f(x) = x

Another similar example for Problem on Relations in Math is:

Let’s assume X is a set of all prime numbers and Y is a set of all integers. Every element from set X is present in set Y, but the opposite is not valid.

Types of Relations

Depending upon the relation between the elements of sets, mathematical relations can be divided into eight types:

• Empty Relation
• Identity Relation
• Universal Relation
• Inverse Relation
• Symmetric Relation
• Reflexive Relation
• Equivalence Relation
• Transitive Relation

Cartesian Product of Sets

(x,y) is the expression of the cartesian product of sets X and Y, such that x ∈ X (x belongs to X) and y ∈Y(y belongs to Y).

For example, if X = {a,b} and Y = {c,d,e}, then the cartesian product of A and B is:

(x,y) = {(a,c), (a,d), (a,e), (b,c), (b,d), (b,e)}.

Function

A relation ‘f’ from a set X to set Y is supposed to be a function of each element of set X that has only an instance in set B.

Miscellaneous Problems on Relations

1.

Answer:

The given relation f:

for 0 ≤ x < 3, f(x) = xٰ²

and

for 3 < x ≤ 10, f(x) = 3x

Also, at x = 3

f(x) = 3×3 = 9 or f(x) = 3 × 3 = 9

That means,

at x = 3, f(x) = 9

Hence,

for 0 ≤ x ≤ 10, the values (images) off are unique.

Hence, it is proved that f is a function.

Now,

for x = 2

g(x) = 22 = 4

and

g(x) = 3 × 2 = 6

Element 2 of the relation g compares to two unique images, i.e., 4 and 6.

Hence, it is proved that relation g is not a function.

2. 

Answer:

It is given that,

f(x) = x²

So,

3.

Answer:

Given function,

It is seen that the function f is characterised for all the numbers except x = 6 and x = 2 as the denominator becomes zero otherwise.

Hence, the domain is R – {2, 6}

4.

Answer:

Given,

f(x) = √(x – 1)

The value of √(x – 1) can be obtained only when (x – 1) ≥ 0.

So, f(x) = √(x – 1) where x ≥ 1.

Thus,

The domain of function f = [1, ∞).

Now,

As x ≥ 1

⇒ (x – 1) ≥ 0

⇒ √(x – 1) ≥ 0

Thus,

Range of function f = [0, ∞).

5.

Answer:

Given,

f (x) = |x – 1|

Clearly,

The function f(x) is defined for all real numbers.

Hence,

The domain of f = R (all real numbers)

Also, for x ∈ R,

Hence,

The range of function f is all positive real numbers.

6.

Answer:

Given,

By substituting the value, we get

The range of f is the set of the entire second item. It is seen that these items are more significant than 0 but less than 1.

As we know,

for x ∈ R,

x² ≥ 0

Then,

x² + 1 ≥ x²

=> 1 ≥ x² / (x² + 1)

Hence, the range is [[0, 1)

7.

Answer:

Given,

f(x) = x + 1

g(x) = 2x – 3

Now,

(f + g) (x) = f(x) + g(x) = (x + 1) + (2x – 3) = 3x – 2

Thus, (f + g) (x) = 3x – 2

(f – g) (x) = f(x) – g(x) = (x + 1) – (2x – 3) = x + 1 – 2x + 3 = – x + 4

Thus, (f – g) (x) = –x + 4

f/g(x) = f(x)/g(x), ( g(x) ≠ 0, x ∈ R)

f/g(x) = x + 1/ 2x – 3, 2x – 3 ≠ 0

Thus, f/g(x) = x + 1/ 2x – 3, x ≠ 3/2

8.

Answer:

Given,

f = {(1, 1), (2, 3), (0, –1), (–1, –3)}

And f(x) = ax + b

For (1, 1) ∈ f

We have, f(1) = 1

Hence,

(a × 1) + b = 1

a + b = 1 …. (i)

And for (0, –1) ∈ f

We have f(0) = –1

a × 0 + b = –1

b = –1

Now, from equation (i), we get

a + (–1) = 1 ⇒ a = 1 + 1 = 2.

Hence,

a = 2 and b =-1.

9.

Answer:

Given,

 R = {(a, b): a, b ∈ N and a = b²}

(i)In this case 2 ∈ N; however, 2 ≠ 2² = 4.

Hence, the statement is false.

(ii) In this case, (9, 3) ∈ N because 9, 3 ∈ N and 9 = 3².

Now,

3 ≠ 9² = 81;

hence, (3, 9) ∉ N

So, the statement is false.

(iii) In this case, (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 4² and 4 = 2².

Now, 16 ≠ 2². = 4;

Hence, (16, 2) ∉ N

So, the statement is false.

10.

Answer:

Given,

A = {1, 2, 3, 4} &

B = {1, 5, 9, 11, 15, 16}

So,

A × B = {(1, 1), (1, 5), (1, 9), (1, 11), (1, 15), (1, 16), (2, 1), (2, 5), (2, 9), (2, 11), (2, 15), (2, 16), (3, 1), (3, 5), (3, 9), (3, 11), (3, 15), (3, 16), (4, 1), (4, 5), (4, 9), (4, 11), (4, 15), (4, 16)}

Also given,

f = {(1, 5), (2, 9), (3, 1), (4, 5), (2, 11)}

(i) This condition is true as the above function is a subset of A × B.

(ii) As the same first item (which is 2) corresponds to two separate images (9 and 11) hence, it is proved that relation f is not a function.

11.

Answer:

Given,

f = {(ab, a + b): a, b ∈ Z}

A relation from a set A to a set B is known to be a function if all elements of set A have distinctive images in set B.

As 2, 6, –2, –6 ∈ Z, (2 × 6, 2 + 6), (–2 × –6, –2 + (–6)) ∈ f

i.e., (12, 8), (12, –8) ∈ f

By looking at it, It’s confirmed that the exact first element, 12, redirects to two different images (8 and –8).

Hence, it is proved that f is not a function.

12.

Answer:

Given,

A = {9, 10, 11, 12, 13}

and f(n) = The highest prime factor of n

So,

3 is the prime factor of 9

2, 5 are the prime factors of 10

11 is the prime factor of 11

2, 3 are the prime factors of 12

13 is the prime factor of 13

Thus, it can be written as

f(9) = 3

f(10) = 5

f(11) = 11

f(12) = 3

f(13) = 13

Hence,

the range of f = {3, 5, 11, 13} where n ∈ A.

Conclusion

The relations in Mathematics are the relationship between two objects. This is a fundamental concept because it can explain how a function works. Further, you can identify whether a relation is a function or not. Relations are primarily used in computer science via comparing two objects. The above-solved problems on relations in math are a few of the basics about function and relation.