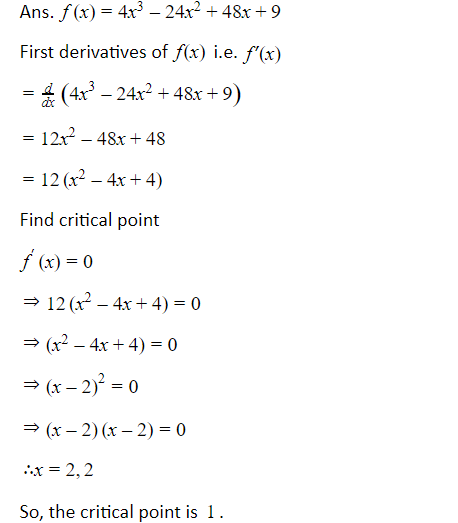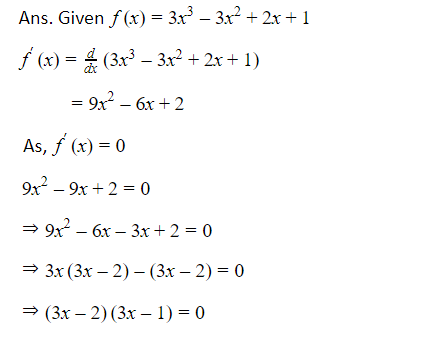At a domain the maximum and minimum value of a function is calculated by taking derivation, this is where the introduction of Maxima and Minima is put into practise.. We find a point at which the value of function is maximum or minimum. If a graph of a function reaches its highest and lowest point are known as maxima and minima respectively.The maximum and minimum values of a function in a closed interval can be arrived at by applying the definition of absolute value.
Let function is defined on a given interval
Let f(x) is defined on an interval I. Then maximum and minimum value of f(x) at a specific point c can be defined as
At x=c if fc≥fx for all values of x in an interval I, then fc=the maximum value of function f(x).
In this case point c is known as a point of maximum value of f(x) in an interval I.
At x=c, if fc≤fx for all values of x in an interval I, then fc=the minimum value of function f(x).
Here, point c is known as a point of minimum value of f(x) in an interval I.
Third condition is an extreme value in interval I. A point c is known as an extreme value of function if at x=c the value of f(c) is either maximum or minimum value.
Local maxima and local minima
Let f(x) is a real valued function and c be an interior point, then local maxima and local minima are defined as
A point c is known as local maxima if h is a positive point and fc≥f(x), for all values of x such that (c-h,c+h).
A point c is known as local minima if h is a positive point and fc≤f(x), for all values of x such that (c-h,c+h).
First Derivative Test:
Let f(x) be a function. Its first derivation is obtained by f’x=ddxf(x). Through the first derivation, we find local maxima and local minima.
If x increases through point c and the value of f'(x) changes from positive to negative i.e. if value of f'(x) is positive at each point near to and to the left side of point c and f’x is negative at each point near to and to the right of point c . So, point c is known as a point of local maxima.
If x increases through point c and the value of f'(x) changes from negative to positive i.e. if value of f'(x) is negative at each point near to and to the left side of point c and f’x is positive at each point near to and to the right of point c . So, point c is known as a point of local minima.
If x increases through point c and the value of f'(x) does not changes, then point c is neither a point of local maxima nor a local minima. Point c is known as “point of inflection.”
Second Derivative Test:
Let f(x) be a function, its first derivation is f’x=ddxf(x) and second derivation is f”x=ddxf'(x). Using second derivation, local maxima and local minima of function f(x) as
Function f(x) is defined on interval I and point c lies in interval I. If f’c=0 and value of second derivative of f(x) at x=c is negative i.e. f”c<0.
Here, point c is known as a point of local maxima and f(c) is the local maximum value.
If f’c=0 and value of second derivative of f(x) at x=c is negative i.e. f”c>0.
Here, point c is known as a point of local minima and f(c) is the local minimum value.
Conclusion:
The approach of determining the maximum and minimum values of a function in a specific discipline is known as introduction of Maxima and Minima. It can be used in practically every line of activity and in almost any subject.
When thinking about the context to represent in terms of a graph, Local maxima are high points for multivariable functions,when they are within sequence to a single variable function. At a limit of a maximum point, the gradient of a multivariable function is equivalent to a zero vector. This corresponds to a graphical representation of a straight tangential plane.When driven by means of a multivariable function f the point of the local maximum is at that point or position in the input space where all other inputs in a narrow region closer to that point generate smaller values.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out