LIMITS OF LOGARITHMIC FUNCTION

The logarithmic function is the inverse of an exponential function. The logarithmic function is defined as below :

y=logax if and only if x=ay ;  for all x>0, a>0 and a≠1

We denote the logarithmic function as,

f(x)=logax    where a is the base of the logarithm.

There are two most commonly used bases. They are base 10 and base e.

When we use the base 10, the function is known as the common logarithmic function and is represented as f(x)=log10x

When we use the base e, the function is known as the natural logarithmic function and is represented as f(x)=logex

The graph of a logarithmic function is as below :

Methods to find the limit of a logarithmic function are discussed below.

LIMITS OF LOGARITHMIC FUNCTION-

When calculating the limit of a logarithmic function, two primary properties are used. The results from these two properties can be directly used as formulas to find the limit. The two properties are :

1. x→0loge(1+x)x=1

2. x→0logb(1+x)x=1logeb

We can also calculate the limit of a logarithmic function using L’ Hospital’s Rule. Let us discuss this rule in detail.

L’ Hospital’s Rule :

According to this rule, for differentiable functions f and g on an open interval I except possibly at a point c contained in I, if 

x→cf(x)=x→cg(x)=0 or ∞ or -∞ and g'(x)≠0 for all x in I with x≠c and x→cf'(x)g'(x) exists, then 

x→cf(x)g(x)=x→cf'(x)g'(x)

Differentiating the numerator and the denominator usually simplifies and converts it in the form that is possible to evaluate directly.

IMPORTANT EXAMPLES

1. Calculate x→elogex-2 / x-2e

To evaluate this limit we will need to deploy the L’ Hospital’s Rule.

Using the L’ Hospital’s Rule, we get

SOME IMPORTANT LIMITS OF LOGARITHMIC FUNCTIONS:

While working on finding limits of logarithmic functions, it is recommended as the best practice to remember some important limits. This will make the calculations faster and easier. Below are some of the important limits.

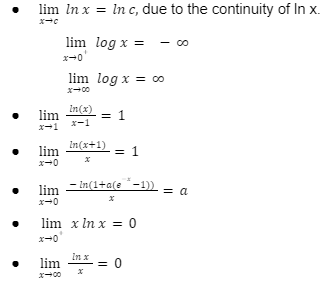
ALGEBRA OF LIMITS-

When solving complex problems on finding limits, it is very important to understand the algebra of limits. It breaks down the problem into simpler limits hence, making it easier to solve. Let us discuss a few theorems of limits and functions which are helpful to solve the problems of limits.

  Special case- if g is constant function such that g(x)=λ, for some real number λ, then

 x→a[λ f(x)]= λ x→af(x)   

CONCLUSION 

Inverse exponential functions are also known as logarithmic functions. Finding the limit of logarithmic functions can become a complex issue without the right knowledge and understanding. We have discussed two methods to find the limit. The selection of the method to solve the problem depends on the complexity of the problem. Most of the problems get solved effectively using L’ Hospital’s Rule. But some questions demand the basic method to solve them. We have also discussed the algebra of limits. The understanding of this concept is a must for everyone because it breaks down complex problems into simpler ones.