A function from a set X to a set Y allocates one element of Y to each element of X in mathematics. [1] The set X is referred to as the function’s domain, while the set Y is referred to as the function’s codomain.

The value of a function f at an element x in its domain is denoted by f. (x).

The set of all pairs (x, f (x)), known as the graph of the function, represents a function uniquely.

When the domain and codomain are both real values, each pair can be considered the Cartesian coordinates of a point in the plane. The graph of the function is a popular way of showing the function and is made up of these points.

An inverse function of a function f (also known as the inverse of f) is a function that reverses the operation of the function f. The inverse of f exists only if and only if f is bijective, and is denoted by f-1if it does.

The inverse of a function f: x-y is f-1: Each element y∊Y is sent to the unique element x∊X in such a way that f(x) = y.

One to One Functions :

One-to-one functions are those that have an inverse.

A function is said to be one-to-one if there is precisely one integer x in the domain of f such that f (x) = y for any number y in the range of f.

To put it another way, the domain and range of a one-to-one function are related as follows:

f-1 domain = f’s range

f-1 range = f’s domain

How to find the Inverse Of the Function ?

The procedure below will assist you in quickly determining the inverse of a function. In this example, we’ll look at the function f(x) = ax + b and try to discover its inverse using the techniques below.

  • Replace f(x) = y with y = ax + b for the given function f(x) = ax + b.
  • To get x = ay + b, replace the x with y and the y with x in the function y = ax + b.
  • For y, calculate the equation x = ay + b. As a result, we get y = (x – b/a).
  • Finally, we can substitute y = f-1(x) with f-1(x) = (x – b)/a.

Graphical Representation :

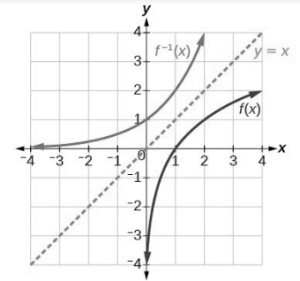
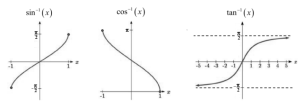
Inverse Trigonometric Functions :

Because the six fundamental trigonometric functions are periodic, they are not one-to-one. However, we may define the inverse of a trigonometric function if we limit its domain to a one-to-one interval. Take the sine function as an example. The sine function is one-to-one on an infinite number of intervals, but the domain is usually restricted to the range[-π2,2]. By doing so, we define the inverse sine function on the domain [-1,1], which tells us which angle θ in the interval [-π2,2] satisfies sinθ  = x for any x in the interval [-1,1].

Examples:

  1. Given the function f (x) = 3x − 2, find its inverse.

f(x) = 3x-2

Replace f(x) with y

y = 3x-2

Swap x with y

x = 3y-2

Solve for y 

y = x/3 + 2/3

Finally replace y with f-1x

f-1x = x/3 + 2/3

  1. Find the inverse for the function f(x) = (3x+2)/(x-1)

Replace f(x) with y

y=(3x+2)/(x-1)

Swapping x and y

x=(3y+2)/(y-1)

Solving y in terms of x

x(y-1)=3y+2

xy-x=3y+2

xy-3y=x+2

y(x-3)=x+2

y=(x+2)/(x-3)

Therefore y=f-1x=(x+2)/(x-3)

Conclusion :

An inverse function is denoted by the signf-1x. If f (x) and g (x) are inverses of each other, for example, we can represent this statement symbolically as:

f(x) = g-1(x) or g(x) = f-1(x)