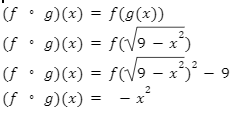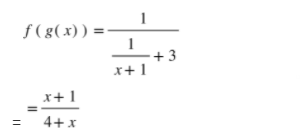Introduction to Composite functions

Functions are commonly used in most mathematical terms such as integration, differentiation, and so on. The function is the relation offset of inputs to a set of possible outputs where every single information is related to one output. 

Composition of functions is a process by which we combine two functions to form the composition of one function with the other. For example, if f(x)=x2 and g(x)=x+1 the composition will be: 

f(g(x))=f(x+1)

=(x+1)2

This function or composition is denoted by a term that is a small circle (), which lies between the functions, like (fg)  and this is read as ‘f composed with g’

Composition of two functions

The composition of the functions f and g is:

(fg)(x)=f(g(x))

The domain of f will be range of g(x) because the domain of  (fg) is the set of all x in the domain of g.

Domain of composite functions

The domain of a composite function is the intersection of the domain of the interior function and the function itself obtained by simplifying the composite function.

Examples:

Example: If f(x)=x+2 and g(x)=4-x2 then solve the following:

1.  (fg)(x)

2. (gf)(x)

3. (gf)(-2)

Solution: 

1. The composition of f with g will be 

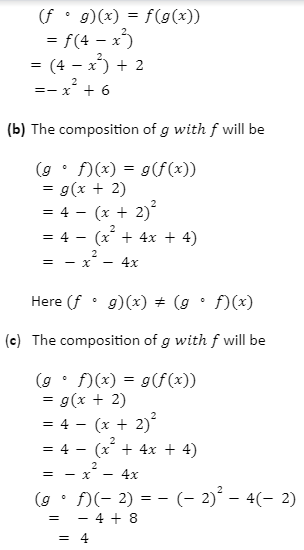
Example: If f(x)=x2-9 and g(x)=9-x2 , find out the domain of (fg) and the composition of (fg)(x)

Solution:

To find the composition of (fg)(x)

Hence the domain of the composition is the set of all the real numbers and is not true. Because the domain of g is -3×3 and the domain of f is a set of all real numbers, therefore the domain of (fg) is -3×3

 Example: Find the composite function and its domain. If f(x)=2×2-x+4 and g(x)=4x+1

Solution: 

Decomposition of functions 

These functions are just the opposite of the composition of functions because in the decomposition of functions, to get a function you will have to break the combined functions into separate elements instead of combining the function. There are several ways to decompose a function, and because of this, the answers can vary from different sources. 

For example, if h(x) =(1-x)3, the inside of the function will be 1-x, and the outside of the function will be x3.

Conclusion

In this section, we learned about the composite functions and how to find their domains. The composition of functions applies one function to the results, and some functions can be decomposed into two or more simple functions. 

Compositions can be widely applicable to arbitrary binary relations, and they are defined in the same way as partial functions, and are always associative. The composition of functions can be easily applied in real life as in the real world, there are many situations in which the quantity depends on a variable that depends on another variable.