Intercept Form of a Line

Introduction

The point where the line or the curve intersects or crosses the coordinate axis on the graph is known as intercept. The point on the line that crosses or intersects the x-axis is the x-intercept and the point in line that crosses or intersects the y-axis is called the y-intercept. Usually, when the axis is not specified we take the y-axis. It is denoted by the letter ”b”.

The slope-intercept form of a line is represented by the equation y = mx+c, where m is the slope, c is the y-intercept of the line, x is the x coordinate and y represents the y coordinate.

Graphical representation of the Intercept Form of a line 

The graphical representation of an intercept form of a line includes the intersection of the coordinate axes at two points. The first intersection is at the x-axis and the second intersection is at the y axis. These two points of intersection are at a distance of ‘a’ and ‘b’ from the x and y-axis respectively.

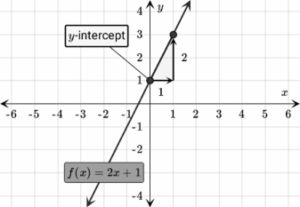
You can calculate this distance from the coordinate axis by referring to the formula of the distance of a point from a line. To measure the shortest distance from the point and the line, a very simple procedure is adopted. It involves drawing a perpendicular line from the point to the given line segment and the length of this perpendicular gives us the shortest distance of the line from that point.

How do you convert the intercept form of a line to the standard form of a line?

The intercept form of a line of an equation is changed into its standard form through a basic formula. The equation of this intercept form is x/a + y/b = 1. 

x/a + y/b = 1

(bx + ay)/ab = 1

bx + ay = ab

The derived standard form of the equation of a line is ax + by + c = 0.

Intercept formula

Equation of the line where the line intersects on the y-axis

y = mx + c

Now, we know that when we write the intercept form of the line we can write b in place of c

y = mx + b

When we make b as the subject of the above formula, it changes as

b = y – mx

where b is the intercept, m is the slope of the line, and x and y represent the x-axis and y-axis at a and b point.

Another way of mentioning this formula is by considering the line intersecting on the x-axis and y-axis at a and b points.

x/a + y/b = 1

Over here a and b are the intercept that intersects the x-axis and y-axis. Over here the value of a and b can be negative, positive, or zero. This depends on the positions of the point where both axes are cut i.e., the relative origin

How Can You Find X and Y Intercepts of a Line?

Take the equation of a straight line equation: Ax + By = C.

To find the x-intercept, put the value of y = 0 and solve the value of x.

To find the y-intercept, substitute x = 0 and solve the value of y.

Example: Consider a straight line with the equation of 3x+2y = 6

To find x-intercept:

Put y = 0 in the given equation

3x + 2(0) = 6

3x = 6

x = 2

To find y-intercept

Substitute x = 0 in the given equation

3(0) + 2y =6

2y = 6

y = 3

Therefore, x-intercept is (2, 0)

The y-intercept is (0, 3)

Two-point form

The formula for the two point form is

Y–y1 / y2–y1 = x–x1 / x2–x1

For example, P(a, 0) = (x1, y1) and Q(0, b) = (x2, y2) are two points taken off the line, which cuts the coordinate axes on the relative position to the origin (0,0). Then the formula becomes:

=> y–0 / b–0 = x–a / 0–a

=> y/b =( x–a )/–a

=> x/a + y/b = 1

Hence, proved.

Slope Intercept Form

The equation having intercept c on the y-axis and having a slope m is

y = mx + c

An important thing to note here is the value of c. It can be positive or negative depending on the intercept drawn on the positive or the negative side of the y axis.

Example 1: 

If we have two intercepts P(2,0) and Q(0,3) and they intersect the x-axis and y-axis, derive the equation of the line.

Solution: Intercepts P(2,0) and Q(0,3) intersect the x-axis and y-axis.

The equation of the line we understand,

x/a + y/b = 1 ……….. (1)

Here, a = 2 and b = 3

Now, substitute the values of given intercepts in a and b from equation 1.

=>x/2 + y/3 = 1

=> 3x + 2y = 6

=> 3x + 2y – 6 = 0,

The equation of the line is 3x + 2y – 6 = 0.

Example 2:

Find the equation of the line, where intercepts make –3 and 2 on the x and y-axis

Solution: We know that, a = –3 and b = 2.

By intercept formula, we conclude that

x/a + y/b = 1

x/–3 + y/2 = 1

or

2x – 3y + 6 = 0.

Hence, this is the required equation.

Example 3:

A-line goes through P(1, 2) and such that its intercept between the axis is bisected at P. What should be the equation of the line?

Solution: The equation of intercepts a and b with x-axis and y-axis are:

x/a + y/b = 1

1 = (a+0)/2 ⇒ a = 2

2 = (0 + b)/2 ⇒ b = 4

Therefore, the equation of line is

x/2 + y/4 = 1

⇒ 2x + y – 4 = 0

Conclusion

​​From the above content piece, the definition of the slope-intercept form should be very clear. The main concept and the logic behind the intercept form of a line and the graphical representation of the intercept form is also discussed above. In addition to these, the intercept formula and the conversion of the intercept form of the line to standard form of the line is also clear from the above explanation. Different forms of representing a line are also discussed such as two-point form besides slope-intercept form. Some solved examples also make the topic very clear to the reader.