Profile
Settings
Refer your friends
Sign out
A geometric progression is a type of progression in which the successive terms have the same constant ratio, known as the common ratio. It is also abbreviated as GP. The GP is commonly represented as a,ar,ar2…., where is the first term and r is the progression’s common ratio. The common ratio can have both positive and negative values. We only need the first term and the constant ratio to find the terms of a geometric series. A geometric progression, also known as a geometric sequence, is a non-zero number sequence in which each term after the first is found by multiplying the previous one by a fixed, non-zero number known as the common ratio.
Geometric progression
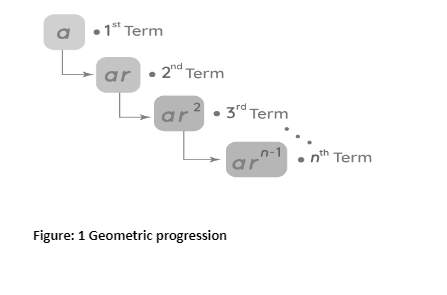
A geometric progression, also known as a geometric sequence, is an ordered list of numbers in which each term following the first is found by multiplying the previous one by a fixed non-zero number known as the common ratio r.
Types of Geometric progression
There are two kinds of geometric progression.
- finite geometric progression
- Infinite geometric progression.
Finite geometric progression: There are only a finite number of terms in a finite geometric progression. It is in the progression that the final term is defined. For instance, 1/2,1/4,1/8,1/16,…,1/32768 is a finite geometric series with the last term being 1/32768.
Infinite geometric progression: There are an infinite number of terms in an infinite geometric progression. It is a progression in which the final term is not defined. For example, 3, 6, +12, 24, +… is an infinite series with no defined last term.
Geometric progression formula
To find the nth term in a progression, use the geometric progression formula. We need the first term and the common ratio to find the nth term. If the common ratio is unknown, it is calculated by multiplying the ratio of any term by its preceding term. The formula for the geometric progression’s nth term is:
an=arn-1
Where, The first term is a.
The common ratio is denoted by r.
n is the number of the term we’re looking for.
Sum of geometric progression
To find the sum of all the terms in a geometric progression, use the geometric progression sum formula. As we saw in the preceding section, geometric progression is classified into two types: finite and infinite geometric progressions, and the sum of their terms is calculated using different formulas.
Finite Geometric Series:
If the number of terms in a geometric progression is finite, the sum of the geometric series is calculated using the following formula:
Sn =a1-rn1-rfor r≠1
Sn=an for r=1
Where, The first term is ” a”.
The common ratio is denoted by r.
n Denotes the number of terms in the series.
Infinite Geometric Series:
An infinite geometric series sum formula is used when the number of terms in a geometric progression is infinite. There are two cases in an infinite series, depending on the value of r. Let’s look at the infinite series sum formula for both cases.
In Case 1: When |r| is greater than one r<1
S∞ =a/(1-r)
Where, The first term is a.
The common ratio is denoted by r.
In Case 2: When r is greater than one r>1
The series does not converge (i.e., it diverges) in this case, and it has no sum.
Geometric progression example
Check to see if the given sequence, 9, 3, 1, 1/3, 1/9……, is in geometrical progression.
Solution: Calculate the ratio of the consecutive terms, a1 = 9 and a2 = 3. So,
a2a1 = 39 =13
= a3a2 = 13
Because the ratio of the given sequence’s consecutive terms is 13 a fixed number, this sequence is in geometrical progression.
Conclusion
Geometric progressions can have finite or infinite lengths. Its common ratio can be either negative or positive. In this section, we will learn more about the GP formulas and the various types of geometric progressions. A geometric progression, also known as a geometric sequence, is a non-zero number sequence in which each term after the first is found by multiplying the previous one by a fixed, non-zero number known as the common ratio.
