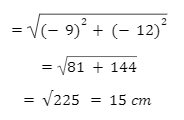How To Check Collinearity Of 3 Points

The term Collinearity means that the points lie on the same line whether they are close together, far apart, or form a ray, line segment, or line. In other words, the set of points is said to be collinear if there exists a linear relation between them, such that the sum of the coefficient in it is zero. 

For example, collinear points can be shown in geometric figures such as ray, line, line segment, triangles, quadrilaterals, parallelograms, etc.

Fig.1. Collinear points

In Fig.1, the points A, B, and C lie on the same line, so they are said to be collinear. 

How to Check Collinearity of 3 points?

The following are the different methods to check the Collinearity of 3 points:

1. Distance formula

2. Slope formula

3. The Area of a Triangle Formula

4. Equation method

Distance Formula

The distance formula is used to calculate the distance between two points whose coordinates are given.

The distance between two points P(x1, y1) and Q(x2, y2) is as follows:

d=(x2-x1)+(y2-y1)2

In this method, three points Q, R, and P are collinear if the sum of the lengths of any two line segments among PQ, QR, and PR is equal to the length of the third line segment:

        PQ + QR = PR

or PR +RQ = PQ

or QP + PR = QR

Slope Formula

The three points are said to be collinear if their slopes are equal.

Let P(x1,y1,z1), Q (x2,y2,z2) and R(x3,y3,z3) be any three points.

Fig.2. Plane 

These three points are collinear if:

Slope of line PQ= Slope of line QR= Slope of line PR

Area of the Triangular Formula

As we know, a triangle cannot be formed using collinear points. So to check the Collinearity of 3 points, the area of the triangle should be equal to zero.

Let P(x1,y1,z1), Q (x2,y2,z2), and R(x3,y3,z3) be any three points.

These points will be collinear if the area of ∆PQR=0:

12x1y2 – y3+ x2y3– y1+ x3y1 – y2= 0

Equation Method

In this method, the three points A, B, and C are said to be collinear only if the third point satisfies the equation through any two of the given three points. 

Collinearity of 3 points in Vector Form: 

The set of points is said to be collinear in the vector form if there exists a linear relation between them, such that the sum of the coefficients in it is zero. 

Necessary and Sufficient Condition of Collinearity of 3 points in Vector Form:
Let a, b, c be the position vectors of three given points.

The equation line passing through points b and  c is:

r= b+ t(c- b)

The points a, b , c will be collinear if:

a= b+ t(c- b)

i.e. if
a- b- tc- b=0

a+(t-1) b-tc=0

The algebraic sum of coefficients =1+t-1+-t=1+t-1-t=0

This is known as the Collinearity of 3 Points in vector form.

Collinear Vectors

The vectors are said to be collinear when they lie in the same direction. Two or more vectors are said to be collinear only if they are parallel to each other in the same or opposite direction. 

Fig.3. Collinear vectors Collinear vectors

in the same direction in the opposite direction

Conditions to Check Collinear Vectors

• Two vectors, a and  b , are said to be collinear vectors if there exists a scalar constant ‘k’ such that  a=kb .  

• Two vectors, a and  b, are said to be in a collinear vector if the ratio of the coordinates is equal. This condition does not exist in the case that one of the components of the given vector is 0.

• Two vectors, a and  b, are said to be collinear when the cross product is equal to the zero vector. It is applicable for 3D vectors only.

Solved Examples

Q 1. Check whether the given points are collinear or not by using the distance formula:  P(8, 11), Q(2, 3), R(-1, -1) 

Solution: Three points, P (8, 11), Q(2, 3), and R(-1, -1), are said to be collinear if:

Distance of PQ+ Distance of QR=Distance of PR

So, PQ+QR=10+5=15 cm=PR

Hence, proved.

Q 2. Prove that the points (2, 4), (4,6), (6,8) are collinear using the Slope Formula.

Solution:  Let P (2,4), Q(4,6), and R(6,8) be the given points.

The slope of PQ  =6-4 /4-2=1

Slope of QR=8-6 / 6-4=1

Slope of PR=8-4 / 6-2=1

Slope of line PQ= Slope of line QR= Slope of line PR  

Hence, A, B, and C are Collinear.

Q 3. Find the value of k if the points P(2,3), Q(4,k), and R(6,−3) are collinear using the Area of the Triangular Formula.

Solution: Points are collinear if the area of ∆PQR=0

⇒12|2(k+3)+4(-3-3)+6(3

k)|=012|2(k+3)+4(-3-3)+6(3

k)|=0⇒12(-4k)=012(-4k)=0

⇒k=0k=0

Therefore, k=0k=0.Let us verify the answer. Area of ΔPQR=1/2|2(0+3)+4(-3-3)+6(3-0)|=0

Conclusion 

The set of points is said to be collinear if there exists a linear relation between them, such that the sum of the coefficients in it is zero. The different methods to check the Collinearity of 3 points are the Distance Formula, Slope Formula, the Area of a Triangle Formula, and Equation Method. 

The set of points is said to be collinear in the vector form if there exists a linear relation between them, such that the sum of the coefficients in it is zero. The vectors are said to be collinear when they lie on the same line. Two or more vectors are said to be collinear only if they are parallel to each other in the same or opposite direction.