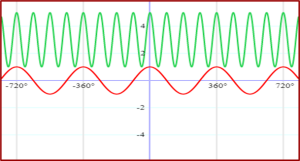
Trigonometric functions are the primary six functions having a domain input value of the angle of a right triangle and a numeric answer as the range. We can work on the domain of the trigonometric function f (x) = sinx, which is the angle represented in degrees or radians with a range of [-1, 1]. Likewise, we have fields and dimensions for all other functions. We use these graphs in many areas of engineering and science. A few examples are the growth of animals and plants, engines, and waves. Besides, we can prepare the graphs for all trigonometric functions. With the aid of the corresponding visual presentation, you may rapidly understand the graphical representations of sine, cosine, and tangent functions. Pupils can learn how to sketch trigonometric functions that are useful to their field of study.

We have six trigonometric functions mentioned below.

1. Sine
2. Cosine
3. Tangent
4. Cosecant
5. Secant
6. Cotangent

What are the trigonometric functions?

We know that sine, cosine, and tangent are the three vital trigonometry ratios based on which functions are defined. Below are some graphs of the three trigonometric functions: sin x, cos x, and tan x. The x-axis values of the angles in these trigonometry graphs are in radians, and the y-axis value of the function at each given angle is f (x).

We can explain the sine trigonometric functions. 

The following is a presentation of a sine graph.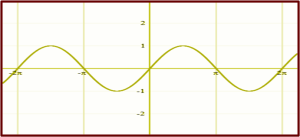

We have values based on trigonometric principles:  

1. As stated above, y = sin x
2. We note here that the roots, or zeros, of y = sin x, are working multiples of π or Pi. 
3. We saw that the sine graph advances along the x-axis as sin x = 0.
4. The period of the sine function is 2π.
5. The peak of the curve at each point is equal to the line value of the sine value.

We can explain the cosine trigonometric functions. We have values based on trigonometric principles.

Presentation of a Cosine Graph, as mentioned below

• y = cos x
• sin (x + π/2 ) = cos x
• The y = cos x graph is the graph we get after shifting y = sin x to π/2 units to the left
• We treat the period of the cosine function as 2π.

We can note here that there are a few analogies between the sine and cosine graphs; they are:

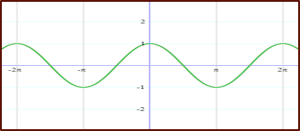
• Both have the same x-axis displacement

• Both have an amplitude of 1

• They have a period of 360° or 2π radians

Tan Graph demonstration:

The tan function isn’t the same as the sine or cosine functions. Throughout π  Radian, the work between negative and positive infinity crosses via 0.

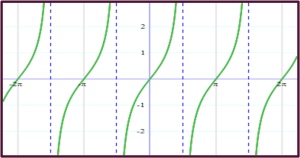
1. As stated on the top, y = tan x
2. As the curve approaches infinity, the tangent graph has an indefinite amplitude
3. We have a period of 180°, i.e.,centre π (Pi)

How do you present all the trigonometric functions graphically? 

The graph below displays a domain value of x on the horizontal x-axis. The same presentation has a range of vertical y-axis in trigonometric function graphs. We note that Sin X and Tan X have graphs that pass through the origin, while other trigonometric functions do not have graphics that go through the start. It is worth noting here that the Sine and Cosine functions in trigonometry have a defined range of [-1, 1].    

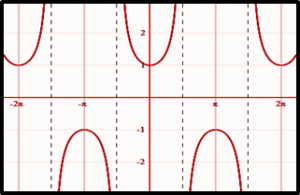
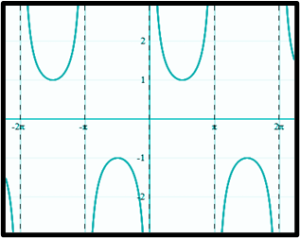
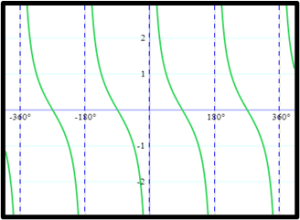
Cosec (X) ⬆   

                                                           COT (X) ⬆

SEC (X)

You can sketch trigonometric graphs for all trigonometry functions if you know the following. 

Amplitude

• It is the absolute value of any number multiplied by its trigonometric function

• We understand that amplitude is the length between the centre line and the peak (or trough)

• You can also measure the height from the highest to the lowest points and divide it by 2

• It tells you how tall or short the curve is

• We observed that the function is in the customary orientation or upside down depending on the minus or plus denotement of the amplitude value.

Period

• Experts treat a period of trigonometric graphs from any point (one peak) to the adjacent matching point.

Phase

• A phase refers to how much is displaced horizontally from its routine location

• It has maximum and minimum turning points

The raised terms are also vital for use in the graph of trigonometry formulas

How to draw the graph of a trigonometric function?

We have different methods for drawing the graph of a trigonometric function. A detailed explanation of one of the efficient methods is below. You can sketch a graph of the sine function. First, convert the objective given to the general form as a sin (bx – c) + d to find the different parameters such as amplitude, phase shift, vertical shift, and period. 

Where,

• |a| denotes amplitude
• Period = 2π/|b|
• c/b denotes phase shift
• Vertical shift = d

Consequently, we may use the cos (bx – c) + d to calculate the cosine function

Example number 1:

Graphing Trig Functions Practice.

y=3sin(2x+ π6) +3 

This means y=3sin(2x+π6) +3 

From the equation, we realise that,

• Period is
• Amplitude is 3 
• Equation moved up by +3 
• And  the distance between the max and min value is 6
• max turning point when (3 × 1)+ 3 = 6 and min turning point when (3× -1) + 3 = 0

Hence Graphical presentation of y=3sin(2x+π6) +3 

 will be as mentioned below,

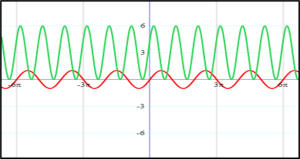
Graphical presentation of the equation y=3sin(2x+π6) +3 

 will be as above. ⬆

Example number 2:

We can also calculate the cosine in degrees. Let the equation y=2cos (4x -2π)+3

• A period is 900
• Amplitude is 2
• The equation is moved up by +3 
• max turning point when (2× 1)+ 3 = +5 and min turning point when (2 × -1) + 3 = +1

Graphical presentation of the equation 2cos (4x -2π)+3 will be as above. ⬆

We quantify the domain of trigonometric operations in degrees or radians. We design the table below that has the most significant trigonometric function values.  We refer to these variables as “standard values,” and we must use them frequently in our computations. Many mathematicians and statisticians use the principal utility of the table. 

Conclusion:

• The core six functions with a domain input value of the angle of a right triangle and a numeric answer as the range are trigonometric functions
• We use trigonometric graphs in many areas of engineering and science
• We can prepare the graphs for all trigonometric Equations
• You may rapidly understand the graphical representations of sine, cosine, and tangent functions