Profile
Settings
Refer your friends
Sign out
A set is a collection of objects/elements, which can be pictorially represented with the help of Venn diagrams. A Venn diagram uses circles and rectangles to demonstrate the relationship between sets and their elements. The universal set is represented by a rectangle, whereas the subsets are represented as circles. The elements of the set are represented within the circle/rectangle itself. A Venn diagram helps us visualise the logical relationship between sets and their elements.
As shown in the image, the universal set U is represented as a rectangle. The elements of the universal set are represented within the rectangle. It can also be presented in roster form as U = {1, 2, 3, 4, 5, 6, 7}.
As shown in the image, set A is represented as a circle. The elements of the set are represented within the circle. It can also be presented in roster form as A = {1, 2, 3, 4, 5}.
Pictorial representation of a subset
The image represents A, which is the subset of the universal set U. The universal set U= {1, 2, 3,…., 8} of which A = {1, 2, 3, 4, 5} is the subset.
The image represents A, which is the subset of the universal set U and set B, which is the subset of set A. The universal set U= {1, 2, 3,…., 10}, of which A = {1, 2, 3, 4, 5} is the subset. The set B = {1, 2} is the subset of set A = {1, 2, 3, 4, 5}.
Pictorial representation of the operation of sets
The types of operation of sets are:
Union of sets
Intersection of sets
Difference of sets
Union of sets
Consider two sets, A and B. The union of set A and set B is denoted as AB. The union of the sets will have all the elements from both sets. The common elements should be considered only once.
In the image shown above, the shaded area represents the union of A and B.
Problems based on union of sets
Let set A = {1, 2, 3} and set B = {4, 5, 6}. Find the union of A and B.
AB = {1, 2, 3, 4, 5, 6}. The union of A and B includes all the elements of sets A and B.
Let set A = {1, 2, 3} and set B = {3, 4, 5}. Find the union of A and B.
AB = {1, 2, 3, 4, 5}. The union of A and B includes all the elements of sets A and B. Since element 3 is presented in both sets, it is considered only once.
Draw a Venn diagram representing the union of set A = {a, b} and set B = {c, d}.
The Venn diagram represents the union of the two sets: set A and set B.
Intersection of sets
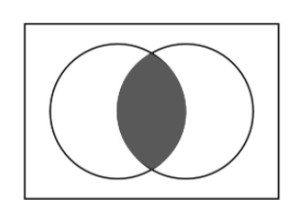
Consider two sets, A and B. The intersection of set A and set B is denoted as AB. The union of the sets will have only the common elements from both sets. In other words, the intersection of two sets, A and B, is the set of all those elements that belong to both A and B.
In the image shown above, the shaded area represents the intersection of A and B.
Problems based on the union of sets
Let set A = {1, 2, 3} and set B = {3, 4, 5, 6}. Find the intersection of A and B.
AB = {3}. The intersection of A and B includes only the common elements of sets A and B. In this case, only element 3 is common in both sets.
Let set A = {1, 2, 3, 4, 5} and set B = {3, 4, 5}. Find the intersection of A and B.
AB = {3, 4, 5}. The intersection of A and B includes all elements of sets A and B. Since elements 3, 4, 5 are presented in both sets, the intersection will have all three elements.
Draw a Venn diagram representing intersection of set A = {a, b, e} and set B = {c, d, e}
The Venn diagram represents the intersection of the two sets, A and B. The shaded portion shows the intersection. The common element e is shown in the shaded part.
Difference of sets
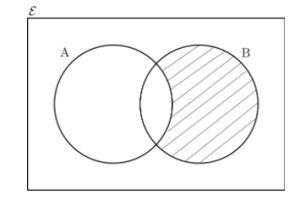
Consider two sets: set A and set B. The difference of set A and set B is denoted as A-B. The difference of the sets will have the elements that belong to A but not B. Similarly, the difference of set B and set A is denoted as B-A.
The difference of the sets will have the elements that belong to B but not to A:
A-B ≠ B-A.
In the image shown above, the shaded area represents A-B.
Problems based on the union of sets
Let set A = {a, b, c, d, e, f} and set B = {b, d, f, h}. Find A-B.
A-B = {a, c, e} since the elements a, c, e belong to A but not to B.
Let set A = {a, b, c, d, e, f} and set B = {b, d, f, h}. Find B-A.
B-A = {h} since the element h belongs to B but not to A.
Conclusion
A Venn diagram is a pictorial representation to demonstrate relationships between two or more sets with the help of overlapping circles and rectangles. It is also used to represent the operations of sets. Venn diagrams are graphical representations for organising and highlighting the similarities and differences between the sets.
