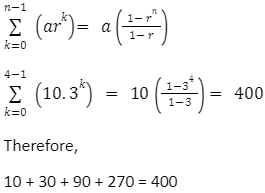A geometric sequence, in algebra, is a set of integers in which the ratio of any two consecutive terms is constant. The common ratio of the sequence is the name given to this constant. For example, 1, 2, 4, 8 is a geometric sequence with a common ratio of 2 and 100. -50, 25, -25/2 is a geometric sequence with a common ratio of -½; however, 1, 3, 9, -27 and -3, 1, 5, 9… are not geometric sequences as the ratio between the consecutive terms varies. More formally, the sequence a₁, a₂…a_nis a geometric progression if and only if  a₂/a₁ = a₃/a₂ = a_n/a_n-1

Amount of n^th term of geometric progression:

A mathematics series is an infinite number of terms with the purpose of maintaining a consistent proportion between the successive terms.

Determination of Sum of Geometric Progression

In a geometric progression, we use a mathematical series of limited terms to infer the equation to track down the quantity of the geometric progression because the typical proportion between the progressive terms is fixed.

For instance, if there are 10 terms in a sequence, and each term is multiplied by the next term, it is known as geometric progression. In this scenario, the number that is subsequently used to multiply is called the common ratio. Whereas in arithmetic progression, when the n^th term is subtracted from (n-1)^th term, there will be a constant difference between any two numbers. Arithmetic progression is written as:

x, x+b, x+2b, x+3b, x+… x+ (n-1) b

Take this sequence: 

3, 6, 12, 24, 48…and it goes on.

6/3= 2

12/6= 2

24/12= 2

48/24= 2

Similarly, for example:

1, ⅓, ⅙, 1/12, 1/24, 1/48…

⅓ / 1 = ½ 

¼ / ½ = ½ 

⅛ / ¼ = ½ 

1/16 / ⅛ = ½ 

1/24 / 1/16 = ½ 

1/48 / 1/24 = ½ 

The ratio between any two successive numbers is the only item that remains constant in the above instances. Geometric progression is the name given to these sequences.

If a sequence x₁, x₂ , x₃, x₄, … x_n is a geometric progression,

a_k+1 / a_k= r (k is always greater than 1)

Here, 

r= is a constant ratio between two numbers 

The n^th term of arithmetic progression was: 

x_n = x+ (n-1) b

In the case of geometric progression let us take 

x is the first number and r is the common ratio between all the numbers. 

The second term will be: x₂= x₁ *r

The third term will be: x₃ = x₂*r = x₁*r*r = xr²

The n^th term will be: x_n = x * r^n-1

The general term will be = x_n = x₁* r^n-1

Facts about geometric progression

• The initial term in a geometric progression is the first number.
• The ratio between a term in the sequence and the term before it is called the common ratio. 

 Common ratio help in determining the nature of geometric progression. 

•   If all terms are of same sign than the common ratio it is because common ratio is positive
• If the terms are alternate positive and negative it is because it’s common ratio is negative 

• If there is exponential growth of terms toward positive or negative infinity it is because it’s common ratio is greater than one.
• If the sequence is constant then common ratio was 1.
• If the common ratio is between 1 and -1 but not equal to zero,then the terms exponentially decays to 0. 
• If the progression is alternate positive and negative with same magnitude of terms its common ratio is -1.
• less than -1, for the absolute value, there is exponential growth towards infinity due to the altering sign. 

Questions

1. 10, 30, 90, 270, 810, 2430…

This sequence has 3 as a factor between each number. 

The value of a and r are: 

a = 10 (the first term) 

r = 3 (the common ratio) 

The rule for any term is: 

x_n = 10 × 3^n-1

The 4^th term is: 

x₄ = 10 × 3^4-1 = 10 × 3³

= 10* 27 = 270

The 10^th term is: 

x₁₀ = 10 × 3^10-1 = 10 × 3⁹

= 10 * 19683 = 196830

2. The sum of the first 4 terms of 10, 30, 90, 270, 810, 2430…

This sequence has a factor of 3 between each number.

The values of a, r and n are: 

a= 10 (the first term) 

r= 3 (the common ratio) 

n= 4 ( sum of the first 4 terms) 

So:

Conclusion 

To find the n^th term in a progression, use the geometric progression formula. We need the first term and the common ratio to find the nth term. If you don’t know what the common ratio is, you can figure it out by dividing any term by its previous term. We must multiply with a set term known as the common ratio every time we want to find the next term in the geometric progression, and we must divide the term with the same common ratio every time we want to get the preceding term in the progression. Example: A GP with a common ratio of 2 is 2, 4, 8, 16, 32, and so on.

There are two types of geometric progressions: finite and infinite. Its common ratio might be either positive or negative.