Profile
Settings
Refer your friends
Sign out
Line equations are an algebraic representation of the set of points in a coordinate system that form the line. Lines consist of many points represented by the variables x and y. These variables are called variables of a line.
The equation of any line can be used to determine whether or not a given point lies on the line. A line equation has a degree of one and is a linear equation. Learn how to find the equation of a line and the different forms of a line’s equation.
Defining the Equation of a Line
It is possible to formulate the equation for a line using the slope and point on a line. An angle’s tangent indicates what is happening at the top of that angle.
The slope of the line is its inclination along the positive x-axis and is expressed as a numeric integer, fraction, or the tangent of the angle it makes with the positive x-axis.
An XY coordinate, i.e. x and y coordinates on the x-axis and the y-axis, are the coordinates of a point in the coordinate system.
This equation can be solved and simplified to a standard form of the equation of a line.
General Equation of a Line
The general equation of a line in two variables of the first degree is given by:
Ax+By+C=0
A, B ≠ 0, where A, B and C are constants that refer to real numbers.
A straight line is always the result of representing the equation geometrically.
The following is an illustration of straight-line formulas in different forms:
Normal Form
The equation of a line whose length of the perpendicular from origin is p and angle formed by perpendicular with positive x-axis is given by α is given by:
x cos +y sin =p
As its name suggests, this is the normal form of the line.
If Ax+By+C=0 is a general line, then it can be expressed in normal form as:
A cos =B sin =-p
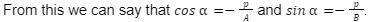
Also it can be inferred that,
cos2+sin2=(p/A)2+(p/B)2
1=p2 [(A2+B2)/(A2.B2)]
- The slope is given by -AB, given that B ≠ 0.
- By multiplying -CAby -CB, we get an x-intercept and a y-intercept.
- From the above discussion, it can be seen that:
- If two points (x1, y1) and(x2, y2)are said to lie on the same side of the line Ax+By+C=0, then the formulas Ax1+By1+C and Ax2+By2+C stand for the same thing. Otherwise, these points would fall across the line from one another.
Intercept Form
A line’s intercept is the point at which it crosses its x-axis or y-axis. The x-axis and the y-axis are respectively cut by a line at (a, 0) and (0, b). A line that has intercepts equal to ‘a’ and ‘b’ respectively on the x-axis and the y-axis is given by:
The equation of the straight line in its general form, i.e., (Ax+By+C=0), if C is not equal to 0, then Ax + By + C = 0 can be written as;
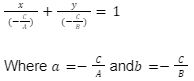
Slope-intercept Form
We know that the slope-intercept form of a straight line is given as follows:
y=mx+c
In this equation, m is the slope of the line and c is its y-intercept.
When B ≠ 0 then, the standard equation of first degree Ax+By+C=0 can be rewritten in slope-intercept form as:
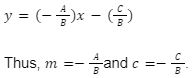
Examples of Straight Lines
The following examples will help you better understand this concept:
Question 1: In general, a line has the equation: 3x-4y+3=0. Determine the slope and both intercepts.
Solution:
We can represent 3x-4y+3=0 in slope-intercept form as follows:
Question 2: An equation of a line is represented by 12x-y+13=0. Compute the slope and both intercepts.
Solution: The given equation 12x-y+13=00 when compared in slope-intercept form gives,
y=12x+13
Matching with y=mx+c,
The slope of the line, m = 12
Reframing the above equation in,
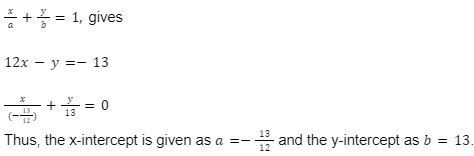
Conclusion
Straight lines follow the equation y=mx+c, where m is the gradient and y = c is the value of where the line crosses the y-axis. On the y-axis, this number is known as the intercept. y=mx+c is the equation of a straight line on the y-axis with a gradient of m and an intercept of c.
There are two main ways to use the equation of a line. First, it is used to define a particular line compactly. Secondly, it can explain how to plot a line in coordinate geometry. For instance, if a specific line needs to be plotted, all the information required will be found in the sentence, “draw the line defined by y=2x+12.”
