Functions are the foundation of calculus in mathematics. The functions are the various types of relationships. In mathematics, a function is represented as a rule that produces a unique output for each input x. In mathematics, mapping or transformation is used to denote a function. These functions are usually represented by letters like f, g, and h. The domain is defined as the collection of all the values that the function can accept while it is defined. The range includes all of the values returned by the function in question. A co-domain is a set of values that have the potential to be outputs of a function. Let’s take a look at the world of functions in math.
Function
A function is a process or relationship that connects each element ‘a’ of a non-empty set A to at least one element ‘b’ of another non-empty set B. In mathematics, a function is a relation f from one set A (the domain of the function) to another set B (the co-domain of the function).
For all an A, b ∈ B, f = (a,b)|
- If every element of set A has exactly one image in set B, the relation is said to be a function.
- A function is a relation from a non-empty set B with the domain A and no two distinct ordered pairs in f having the same first element.
- If A B and (a,b) ∈ f are functions, then f(a) = b, where ‘b’ is the image of ‘a’ under ‘f’ and ‘a’ is the preimage of ‘b’ under ‘f’.
- If there is a function f: A → B, the set A is referred to as the domain of the function f, and the set B is referred to as its co-domain.
Types of function in math
The function y = f(x) is classified into different types based on factors such as a function’s domain and range, as well as the function expression. The domain x value of the functions is referred to as input. A number, angle, decimal, or fraction can be used as the domain value. Similarly, the range is represented by the y value or the f(x) value (which is usually a numeric value).
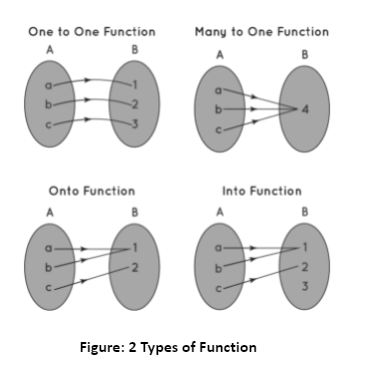
In general, there are six types of functions.
- One to One (Injective) function.
- Many to One function.
- Onto (Surjective) Function.
- Into Function.
- One to One Onto Functions
- Many to One Into Function.
One to One (Injective) function.
If the images of distinct elements of X under f are distinct, a function f: X -> Y is said to be a one to one function. As a result, f is one to one if f(x1) = f (x2).
Many to One function.
If the function is not one to one, it should be many to one, which means that each element of the domain has more than one image at the codomain after mapping.
Onto (Surjective) Function
An onto function is one in which every element of Y is an image of some element of set X under f, i.e. for every y ∈ Y there exists an element x in X such that f(x) = y.
Into Function
A function f: X -> Y is said to be an into a function if there are at least one or more elements in Y that do not have any pre-images in X, which simply means that no elements of the codomain are mapped with elements of the domain.
One to One Onto Functions
If a function f: X-> Y is both One to One and onto, it is said to be a bijective function.
Many to One Into Function.
If a function f: X-> Y is both Many to One and into, it is said to be a Many to One Into function.
Objective function in math
To solve optimization problems, the objective function is required. An objective function is a linear representation of the form Z = ax + by, where a, b are constraints and x, y are variables that must be maximized or minimized. The decision variables are variables x and y. A few constraints control an objective function, some of which are x > 0, y > 0.
The objective function of a linear programming problem is required to find the optimal solution: maximize profit, minimize cost, or minimize resource use, right resource deployment. The objective function in LPP is widely used to represent problems in commerce, industry, and applied sciences.
- Theorem 1: For a linear programming problem, let R be the feasible region (convex polygon) and Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where x and y are variables are constrained by linear inequalities, this optimal value must occur at a workable region’s corner point* (vertex).
- Theorem 2: For a linear programming problem, let R be the feasible region and Z = axe + by be the objective function. If R is bounded**, the objective function Z has a maximum and a minimum value on R, both of which occur at a corner point (vertex) of R.
Objective Function Applications
The objective function can be used in a variety of ways, as shown below.
Manufacturing Issue: The number of units of various products produced by a manufacturing firm is determined by machine time, man hours, and warehouse space per unit item. All of this must be taken into account when attempting to solve the problem of minimizing costs and allocating necessary resources.
Diet Problems: A linear programming problem that can be solved using an objective function is the proportion in which the different constituents of the diet are to be included in the food in order to optimize the nutrients received while also lowering the cost of the diet.
Transportation Problem: The various routes that must be followed in order to reduce distance, increase the number of dropping points, and reduce fuel cost is an optimization problem that can be presented as an objective function and solved for the best solution.
Conclusion
A function is a mathematical expression that connects an input to an output. It is analogous to a machine with an input and an output. and the output is somehow related to the input. Functions are mathematical building blocks used in machine design and prediction of natural disasters, disease cures, global economic understanding, and human flight aero planes. Functions can take input from multiple variables and always produce the same output, which is unique to that function.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






